|
『コロンブスの電磁気学』増補改訂版(A4判 831頁 価格:6000円) |
|
『コロンブスの電磁気学』増補改訂版(A4判 831頁 価格:6000円) |
敬愛するマイケル・ファラデー(9) 縦列接合がコイルの謎を解く
2011年2月12日
宇佐美 保
先の≪敬愛するマイケル・ファラデー(7) 縦列接合がコンデンサの謎を解く≫に於いては、コンデンサ(フィルタ・タイプ)は、入力側伝送路並び出力側伝送路に「縦列接合された伝送路」であることを明らかにしました。
又、前の≪敬愛するマイケル・ファラデー(8) 縦列接合以外のコンデンサ≫に於いては、「縦列接合」以外にも、「並列接合」、「直列接合」された伝送路もそれ相応のコンデンサとしての機能を果たす事を証明して来ました。
これらの結果から、従来「(まるで魔法の小箱のように)電荷を蓄える電気部品(素子)」と教えられて来たコンデンサが、単に「低特性インピーダンスの伝送路」であると確認できたのです。
では、コンデンサ同様に「磁束を蓄える電気部品(素子)」と、これまた“まるで魔法の小箱のように”教えられて来たコイルはどうなのでしょうか?
しかし、この「魔法の小箱」も次の「写真:1-1〜-4」のコイルを用いての簡単な実験で、その小箱の中には魔法なんか存在しないことが分かります。
実測に使用したコイルは、市販のFMチューナに使用されているコイル(6巻きしたコイル:写真:1-1)と、手製の紙ボビン(直径:10mm)にエナメル線(0.3mmφ)を6巻き巻き付けます(写真:1-2)。
この他に、ジグザグ巻き(写真:1-3)にした場合、単に平面を往復させた場合のコイル(ここで、更には、平面型(写真:1-4))を準備しました。
(形状から申しまして、この2者を現状ではコイルと言えるのかは別としまして)
これらの各コイルに、パルスジェネレータからクロック信号(500mV)を1パルスのみ同軸ケーブル(Z=50Ω)入力して、その出力信号を同軸ケーブルで、オシロスコープに導き測定し、これら測定しました4種類のコイルとも、程度の差こそあれ、それなりにコイルの性格を示しています。
(即ち、入力されたクロック信号は、コイルを通過する事によって、その信号の立ち上がり/立下り部が鈍化している事が分かります)
その結果を次に示します。
この測定結果をご覧になって従来のコイルに関する概念「コイルは磁界を蓄える」では、解釈できないことが発生していることにお気づきと存じます。
なにしろジグザグ巻きでは、右巻き、左巻きのコイルが連続的に登場しますから、これらのコイルに生じる磁界の方向は互いに逆向きですから、それらの磁界はお互いに打ち消し合ってしまいます。
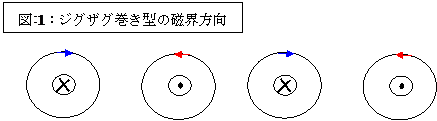 |
(×印は磁界が紙面の反対側へ向かっている事を示し、・印は磁界が紙面の手前に向かっている事を示しています)
従って、コイルは「磁界を蓄える魔法の小箱」ではない事がはっきり認識できるのです。
何故このような誤解が長い年月の間罷り通ってきてしまったのでしょうか?!
それは、「電気は、プラスからマイナスへ向かって運ばれる」と教えられ続け、信じ込んできたからです。
この件は、≪『コロンブスの電磁気学』増補改訂版の概略≫の「1 電気の流れ(シングルエンド的な流れではなく、伝送路的な流れ)」をご覧頂ければすぐにお分かり頂けますように、電気は「いわゆる信号線」を伝って、最後には「いわゆるグランド線」に流れ込んで行くのではなく、電気は「信号線」、「グランド線」を同時に進行する事に気が付かれます。
そこで、コイル(「写真:1」)を信号線にセットして、その信号線とペアを組む「グランド線(一般的には直線です)」を考えますと、不思議な事が起こります。
何しろ、コイルを経由しての、コイルの入出力間の信号線の長さは、当然グランド線の長さより長くなります。
これでは“電気は「信号線」、「グランド線」を同時に進行する事”が出来なくなります。
そこで、「電気は電荷が運ぶ」との神話を氷解させた、「電流は電磁波川と導体堤防の共同作業」それに続く、先に説明させて頂いた「縦列接合」の発見を思い起こして下さい。
そして、この「縦列接合」の概念を導入する事で、変位電流が流れると長年信じられて来たコンデンサも「魔法の小箱」ではなく、「縦列接合された伝送路」である事が解明されました。
そして、コイルに関しても「縦列接合」の概念によって、「魔法の小箱」ではなく、「縦列接合された伝送路」である事が解明されるのです。
特に、「写真:1-4(平面型コイル)」をご覧いただければ、この平面型コイルは、3本の伝送路が縦列結合されているにすぎない事がお判りと存じます。
しかし、平面型はともかく「コイルは別物」と思われるでしょうが、次の各図、並び写真をご覧ください。
即ち、先ずは「図:2」のコイルから「図:3」に示しますように、入口部の交差解消するように一捻りするのです。(分かり易いように、左側部分を2点差線で表示しました。)
 |
こうなりますと、「図:3」の状態は、次の「図:4」の縦列接合された一般的な伝送路を左右に開いた状態と同じとなります。
 |
この図面的な考察から、コイルは入出力伝送路に縦列接合された(しかも信号線グランド線間を距離的に開かれた)伝送路であることが判ります。
次の写真:2で、「1巻きコイル」→「1巻きコイルの連続」→「3巻きコイル」と「連続した1巻きコイル」の中継線が短くなると「3巻きコイル」と変化するのです。
| 写真:2 | ||
このコイルの概念的な写真から、信号線とグランド線を堤防とする電磁波川の流れが、これらの堤防と縦列接合されているコイルの堤防が形成するコイル伝送路に流れ噛んでゆく様子がイメージできるのではないでしょうか?
その際大事な法則(ファラデーの偉大な発見「電気は近接作用である」)を思い出して下さい。
縦列接合地点から、コイル伝送路に電磁波川が流れ込んできたら、その先が開いていようが関係なく、その流れは継続されるのです。
(コンデンサであろうとコイルであろうと、その末端がオープン状態であろうと、ショート状態であろうと!)
尚、“コイルは環状であって直線ではない”と思われる方もございましょうが、逆手に取って申し訳ありませんが、コイルを説明される場合用いられた式は、「ファラデーの電磁誘導式」であって、この式には形状的因子はありません。
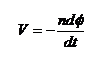 |
しかし、実際には形状によって異なるのです。この点は後に掲げる「測定結果:5&6」等で考察いたしますが、一点だけ前以って留意しなくてはならない点があります。
それは、伝送路が環状となることで、伝送路を形成する2本の導体間の距離が増大し、その結果伝送路の特性インピーダンスも増大する事です。
そして、伝送路がコイルとして機能する為には、この伝送路の特性インピーダンスの大きい事が不可欠なのです。
そこで、特性インピーダンスの大きな伝送路として、その値が300オームである(リボン型)フィーダー線(アンテナの給電線:feeder)を「図:5」のように、入出力側伝送路としての同軸ケーブル(Z=50オーム)に、縦列接合して、電源(パルスジェネレータ)から、電気信号を送り出し、以下の測定を行いました。
| 図:5 |
先ずは、パルスジェネレータから、10MHzのクロック信号(1ボルト)を1パルスこれらの伝送路系に送り出し、各箇所での電圧変化を測定し「測定結果:2」を得ました。
| 測定結果:2 |
この結果(特に、「出力伝送路へでの電圧変化波形」)を見ますと、入力されたクロック信号の立ち上がり立下り部の鈍りが観測されており、このフィーダー線が、立派にコイルとしての役割を果たしている事が分かります。
そして、又、先のコンデンサの場合同様に、各部での電圧変化が段階的であることも、見てとれますので、コイル入口部での変化を拡大して観測した結果を次の「測定結果:3」に掲げます。
| 測定結果:3 |
この結果をみると、明らかに先のコンデンサの場合同様に、電圧変化は段階的な(入力信号がON/OFFされた時に正負対称的な)変化を呈している事が分かります。
更には、先の「測定結果:2」に於いて、コイルの場合でも、コイル接合部から入力側への逆流電流が観測されておりますので、コンデンサの場合同様に、入出力伝送路である2本の同軸ケーブルの長さを共に、10メートルとして、且つ入力信号の波長を短くする為に、その周波数を50MHz(1ボルト)とし、1パルス送りこんだ場合の測定結果として「測定結果:4」を得ました。
| 測定結果:4 |
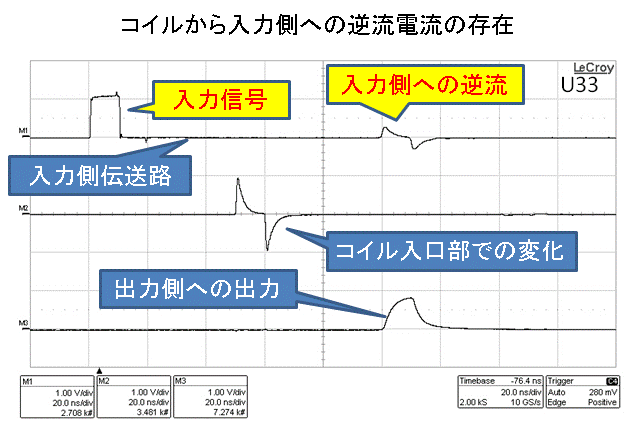 |
このように、コイルの場合もコンデンサの場合同様に、入力が波への逆流電流が観測されています。
私達は、“「ファラデーの電磁誘導式」の係数にマイナス符号が付いている事から、
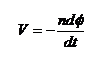 |
自然は変化を嫌うので、コイルに電流が流れると、その変化を打ち消すように、コイルはマイナスの電流を発生する”と教わりましたが、出力側はそうとも思えますが、入力側への逆流電流の存在を説明されませんでした。
(それも、逆流電流はコイル内の磁束が増大する際には、プラスとなっております)
と言う事は、この点からも従来のコイルに対する認識が誤解であったことが分かります。
そこで、先の≪敬愛するマイケル・ファラデー(7) 縦列接合がコンデンサの謎を解く≫の場合同様に、イメージ図を用いて、コイルの働きに関して考察いたします。
このコイル伝送路と出力伝送路が入力伝送路に縦列接合されている状態で、入力伝送路側からクロック信号が入力された場合の各伝送路での電流(電磁波川の流れと導体堤防間の相互作用)の流れ具合の「イメージ図:1」を先ずご覧ください。
| イメージ図:1 |
ここでは、入力側並びに出力側の伝送路の特性インピーダンスが等しくZであり、コイル伝送路のそれがZc(但し、Zc≫Z)とすると、入力伝送路から流れて来た電流は、殆ど反射して戻りますが、残りの僅かな電流は、コイル伝送路と出力側の伝送路に、そのまま両者等しく流れ込んで行きます。
(尚、先のコンデンサの場合同様に、表示場所の関係から、コイル内の電圧幅(本来なら、ここでのZは大きいので電圧幅は広く書かなくてはなりませんが、それでは画面からはみ出してしまいます)、時間軸は入出力側(コイル部と同じにしますと、これまた画面からはみ出してしまいますので)と異なって表示してあります。
更には、今回のコイル伝送路の場合も、先のコンデンサ伝送路の場合同様に、出力側伝送路とともに入力側伝送路に「縦列接合」されていますから、反射係数式などは皆コンデンサの場合と同じです、ただ異なるのは、コイル並びコンデンサ伝送路自体の特性インピーダンスが大きいか小さいかの相違だけです)
そして、もう一点の相違点が、それら伝送路の末端がショート状態か、オープン状態かの違いです。
従って、今回のコイル伝送路の末端はショート端ですから、プラス電流として末端に向かった電流はマイナス1の反射を受けて、マイナス電流としてコイル伝送路の入口部へ戻って行きます。
この結果、「イメージ図:2」を御参考頂きたいのですが、コンデンサの場合と異なって、出力伝送路へは、プラス電流が、入力側伝送路へはマイナス電流が排出されます。
| イメージ図:2 |
又、ここでも当然、反射を受けますが、その際、コイル伝送路がコイル機能を発揮する為に大事な点は、反射係数(τc)が、次式に示されるようにマイナスの値である点です。
(コンデンサの場合はプラスの値でした)
(∵ Zc≫Z 今回の場合は、前者が300Ωで後者が100Ω(=50+50))
従って、又、ここでの反射電流もマイナス反射を受け、(当初入力伝送路から直接入力されたプラス電流同様)プラス電流として末端へ向かいます。
このようにして、コイル伝送路入口部では、プラス電流が末端へ向う電流と、末端でマイナス電流となって戻り、直ちに、プラス電流となって末端へ向かう電流が、行き来する結果、「測定結果:3」のコイル入口部のステップ状電圧波形が観測されます。
このようにコイル内に入った電流は両端で反射を繰り返しますが、入口部では、入出力側伝送路に、その一部を排出する為、反射回数の増大とともに(コンデンサの場合同様に)「イメージ図:3」にご覧頂けますように、その電流値は小さくなって行きます。
| イメージ図:3 | イメージ図:4 |
そして、最終的には、「イメージ図:4」のように、入出力側伝送路への排出電流も飽和状態、そして、コイル内電流の先頭はゼロに収束して行き飽和状態となり、これらコイル内電流(電圧)の合算値も当然ゼロに収束します。
但し、ここで注意しなくてはいけないのは、コイル内電流(電圧)の合算値も当然ゼロに収束したからと言っても、コイル内の電流が消滅したのではなくて、入口からは常に入力伝送路側からの電流が流れ込んでおり、入口部と末端での反射を繰り返し続けているのです。
そして、コイル内の磁界の向きを考えますと、プラス(磁界が右ネジ方向)で末端へ行った電流はマイナス(磁界は左ネジ方向)で帰ってくるため、コイル内の磁界の向きは、常に、末端へプラス電流が向かっている状態(右ネジ方向の磁界)が維持されるのです。
この点から、“コイルは磁界を蓄える”と言う事になるのです。
一方、電界に関しては、行きのプラス電流と帰りのマイナス電流の電界がキャンセルしてしまい、“コイルは電荷を蓄えるとの言葉が存在しなかった”のです。
ところが、コンデンサの場合は、末端並び入口部での反射は、プラス反射ですから、プラスでコンデンサ伝送路に入った電流は、常にプラスで存在し続けます。
ですから、コンデンサ内には常にプラス磁界が存在し、その結果“コンデンサは電荷を蓄える”との言葉が今まで生き延びて来たのです。
ところが、磁界に関しては、プラス電流がコンデンサ伝送路の入口部末端部を常に往復していますから、行きの磁界と帰りの磁界が相殺し、“コンデンサは磁界を蓄えるという言葉が存在しなかった”のです。
では、先のコンデンサの場合同様に、ここまでのイメージ図を活用してのアニメーションをご覧ください。
 |
|
次は、コイル伝送路が飽和状態の後に、入力信号がオフとなり、信号が縦列接合点へ来なくなった時点からの変化です。 |
先ずは「イメージ図:5」の如く、入力側の伝送路への反射波はなくなります。
| イメージ図:5 |
そして、入力伝送路からの出力側の伝送路へ、又、コイル伝送路への信号の流入も途絶えます。
次は、コイル伝送路が飽和状態の後に、入力信号が縦列接合点へ来なくなった時点からの変化です。
先ずは「イメージ図:5」の如く、入力側の伝送路への反射波はなくなります。
そして、入力伝送路からの出力側の伝送路へ、又、コイル伝送路への信号の流入も途絶えます。
それでも、コイル伝送路内で反射を繰り返している電流からは、入出力側の伝送路への電流の排出はしばらく続きます。
ところが、「イメージ図:6」のように、新たにコイル伝送路への流入は途絶えていますから、反射回数が0回目、1回目、2回目と反射回数の少ない電流からどんどん(しっぽを切られるように)消滅して行きます。
| イメージ図:6 | イメージ図:7 |
そして最後は、「イメージ図:7」のように、コイル伝送路内の電流もすべて消滅して、入出力側の伝送路への電流の排出も完全になくなります。
これらの様相の変化を次のアニメーションでご覧下さい。
 |
此処までの、コイル伝送路は、直線的(フィーダー線そのまま)でしたが、次は、そのフィーダー線の2本の銅線の距離を一定に保っているリボン状の樹脂部分を取り除き、導線を環状の伝送路に仕立てて、直線の場合(「図:5)同様にセットし、1MHz(1ボルト)のクロック信号を1パルスを流して、コイル入口部での電圧変化(信号ON時とOFF時)を「直線の場合」と「環状の場合」を比較した結果を「測定結果:5」に掲げます。
| 測定結果:5 (上の2者は直線の場合、下の2者は環状の場合) |
この原因は、伝送路を環状にすることで、電流の進行につれ、2本の導体間隔が常に変化していますから、その部分の特性インピーダンスを変化します。
特性インピーダンスが異なれば反射現象が発生しますから、電流は反射を繰り返しながら(多重反射しながら)コイルの入口部末端部を往復するので、全体としての往復時間も長くなり、当然電圧変化も緩やかになります。
そこで、一般的な表現では、コイルのインダクタンス値が大きくなるという事になります。
従って、「測定結果:6」に見ますように、両者の出力波形を比較すれば、環状コイルの場合の方が、波形変化も緩やかになります。
(ゆっくり上昇して、ゆっくり下降しています)
| 測定結果:6 |
尚、今回のコイルは、直線にしても環状にしても、1巻きコイルに相当しますが、このコイルの巻き数を増加させると、コイルは、縦列接合されている伝送路と見なされますから、それら何巻きも巻かれたコイル伝送路の合算特性インピーダンスは、その巻き数に比例する事になり、入力伝送路側から見たコイル伝送路入口部での反射係数は、よりマイナス1に近づき、反射を繰り返すことによるコイル内電流値の絶対値の減少速度は小さくなり、又、入力伝送路側から見た反射係数はよりプラス1に近づき、ほとんどは入力側へと戻り、コイル伝送路(出力伝送路)へ入り込む電流値も小さくなりますから、この点からも、コイルのインダクタンス値は増加します。
尚、コイルの巻き数を増やすと、コイル伝送路を流れる電流(電磁波川の流れ)は、先の≪敬愛するマイケル・ファラデー(5) 縦列接合の登場≫にて説明しましたように、複雑化して行きます。
(勿論、コイルの巻き数がnになれば、これら、1巻きずつのコイルは互いに入力伝送路に対して縦列接合されていますから、特性インピーダンスは、一般的には1巻きの場合に比べてn倍にはなりますが、
「ファラデーの電磁誘導式」に於いて、コイルの巻き数がnであるから、1巻きの場合に比べて、コイル的機能が、n倍となるような単純な話ではないのです)
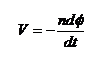 |
この件等を含めまして、色々と気になる点がおありでしたら、是非とも『コロンブスの電磁気学』増補改訂版をご参照ください。
(コイルの章も、各種の実験結果などを掲載したりして、A版で80数ページ費やしておりますから)
最後にくどいようですが、一般的なコンデンサとコイルの相違を次の表に纏めて見ます。
| 一般的なコンデンサとコイルの相違 | |||||
| 縦列接合された伝送路 | 従来言われていた以下のような 「魔法の小箱」ではありません |
||||
| 特性インピーダンス | 末端状態 | 入口部と末端を往復する電流 | |||
| コンデンサ | 小 | オープン | プラス/プラス | 電界が同方向 | 電荷を蓄える「魔法の小箱」ではありません |
| コイル | 大 | ショート | プラス/マイナス | 磁界が同方向 | 磁束を蓄える「魔法の小箱」ではありません |
では、今回も余り長くなりましたので、次の≪『コロンブスの電磁気学』の要旨(10) 直列接合のコイル(敬愛するマイケル・ファラデー(10) 直列接合のコイル)≫に続けさせて頂きます。
|
『コロンブスの電磁気学』増補改訂版(A4判 831頁 価格:6000円) |