敬愛するマイケル・ファラデー(8) 縦列接合以外のコンデンサ
敬愛するマイケル・ファラデー(8) 縦列接合以外のコンデンサ
2011年2月11日
宇佐美 保
前の≪敬愛するマイケル・ファラデー(7) 縦列接合がコンデンサの謎を解く≫に於いては、入力側伝送路へ出力側伝送路と共に縦列接合されている状態のコンデンサについて考察しました。
そこで今回は、「縦列接合されている状態」以外のコンデンサに関して考察します。
| 「その1:並列接合されている状態のコンデンサ」 |
次の「図:1」のように、入力側伝送路へ出力側伝送路と共に並列接合されている状態のコンデンサについて考察します。
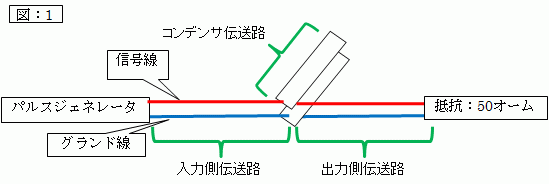 |
このように接続されているコンデンサは、バイパス・コンデンサと称されております。
そしてこのバイパス・コンデンサの一般的な概念(“高周波ノイズの混ざった直流をバイパスに設置したコンデンサによって、高周波ノイズのみをグランド(一般的にはアース線を介して地球に)に逃がし、直流のみを本流の電気回路に流す”)を「図:2」に示します。
(図のコイルは、高周波信号を遮断し、バイパス・コンデンサへ送り返す役割を演じる)
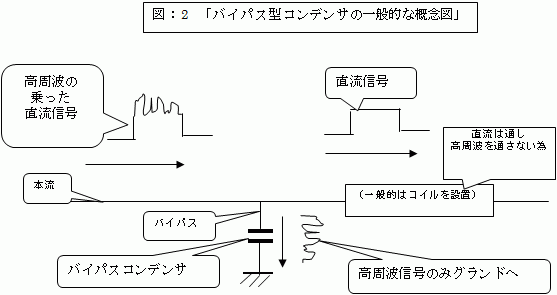 |
(このような図は、昔、ラジオを組み立てた際、交流を整流器にて直流に変換させた後に、その直流中に残存する高周波成分を除去する為の平滑回路としてご記憶と存じます)
でも、はっきり申しまして、従来のバイパス・コンデンサの概念(又、この概念図)は真っ赤な嘘です。
なんと申しましても、高周波信号がバイパス・コンデンサを通して、グランドに流れるのは、「シングルエンド」的発想です。
そこで当初に掲げた「図:1」の並列接合された伝送路として考察してみましょう。
先ずは式を使わず(式が出てきても、それがお嫌いな方は、前文同様に、その式に対して、目をつぶられても結構です)に概念的な解釈を行います。
そこで、先の縦列接合の場合と同様に、今回の並列接合の場合として次の3点を頭の中にお入れ下さい。
| 先ずは、一般的な伝送路の反射現象に関する1点です。 |
|
| 1. |
特性インピーダンスの異なる地点では、電流の反射現象が生じます。 しかし、この反射地点のその前後の伝送路での電圧は等しくなります。 (入力電流+反射電流)×入力側伝送路の特性インピーダンス =(反射点先電流(=入力電流−反射電流))×反射点先の伝送路の特性インピーダンス |
| 次は、「並列接合」に関する私の見解の2点です。 | |||||
| 2. |
並列接合された伝送路の合成特性インピーダンスは、並列接合された抵抗の合成値同様な関係が存在します。 (注:入出力伝送路の特性インピーダンスは同じZ、コンデンサ伝送路のそれをZcとしますと、合成特性インピーダンスZs は次のようになります。
|
||||
| 3. | 並列接合では、並列された伝送路には、同一電圧値となる電流が流れる。 | ||||
この点を留意して頂き、次の「イメージ図:1、2&3」をご覧ください。
| イメージ図:1 |
入力側伝送路に、並列接合された出力側伝送路とコンデンサ伝送路へは、それらの分岐路から、同一電圧の電流が流れます。
そして、入力伝送路から、これら並列接合された伝送路の合成インピーダンス(Zs)は、先の(式:1)から、殆どZc(≒0Ω)に見えます。
ですから、分岐路では、ほぼマイナス1に近い反射が行われる事になり、分岐路点の電圧は、極端に小さい値、即ち、出力伝送路コンデンサ伝送路へ流れる電流の電圧も極端に小さい値となってしまいます。
尚、入力伝送路側からの反射係数(τ)は次のようになります。
そして、出力伝送路へ流れ出た電流はそのまま出力伝送路を流れ続けて行きますが、コンデンサ伝送路に侵入した電流は次のイメージ図に見るように(又、先の縦列接合の場合同様に)その伝送路の末端まで行き、完全反射されて次の「イメージ図:2」のようにコンデンサの入口部へ戻ってきます
| イメージ図:2 |
そして、このコンデンサ入口部では、コンデンサ伝送路の特性インピーダンス(Zc)に比べて、その先に並列接合されている入出力伝送路の合成特性インピーダンス(Z/2)が格段に大きいので、ほぼ1に近い反射現象が起こり、大部分の電流はコンデンサ伝送路を又末端へと戻って行きます。
そして、入出力伝送路へは、その反射現象で生じるコンデンサ伝送路末端部の電圧と各々等しい電圧を示す電流が流れて行きます。
尚、この際の反射係数(τc)は次の式で表す事が出来ます。
しかし、コンデンサ伝送路では、先の縦列接合されたコンデンサ伝送路と同様に、電圧は、時間の経過と共に、(このコンデンサ伝送路の末端もオープン状態ですから)徐々に増大し、次の「イメージ図:3」に見ますように、出力伝送路へ(入力伝送路へも)排出する電流の電圧も増大して行き、最終的には、このコンデンサ伝送路へ入ってくる電流と排出される電流の電圧が同一となって、コンデンサ伝送路内の電圧は飽和状態となります。
| イメージ図:3 |
この状態では、このコンデンサ伝送路は無いに等しい状態となりますから、入力伝送路から(コンデンサ伝送路の存在を全く無視して)出力伝送路へ電流は流れて行きます。
(しかし、飽和状態のコンデンサといえども、そこに高周波信号が加算されて到達すれば、その分は新たな電圧変化分ですから、この電圧変化分は、先と同様に分岐路では、ほぼマイナス1の反射が行われキャンセルされてしまいます)
このようにして、高周波信号は、バイパス・コンデンサ伝送路によって、出力伝送路への流れが、相殺されているだけです。
(それでも、結果的には拒否された状態となりますが)
そして、以上の考察が、直流がバイパス・コンデンサ伝送路の存在を無視して出力伝送路へと流れる考察にもなるのです。
更には、入力信号がオフとなった後も、先の縦列接合の場合同様に、コンデンサ伝送路からの排出電流が段階的に減少して行くことは明らかです。
この様相を、先の縦列接合の場合に用いたコンデンサを「図:1」のように、並列接合して、次なる実験で確認しましょう。
電源(パルスジェネレータ)から、1MHz(1ボルト)のクロック信号を1パルス、出力して次の各種の測定を行いました。
次の「測定結果:1」から、「イメージ図:1、2並びに3」に示される各伝送路に於いてステップ状に電圧が変化する様子(又、コンデンサ伝送路の末端では、最初のステップが完全反射の影響で、他のステップより2倍ほど高くなっております)
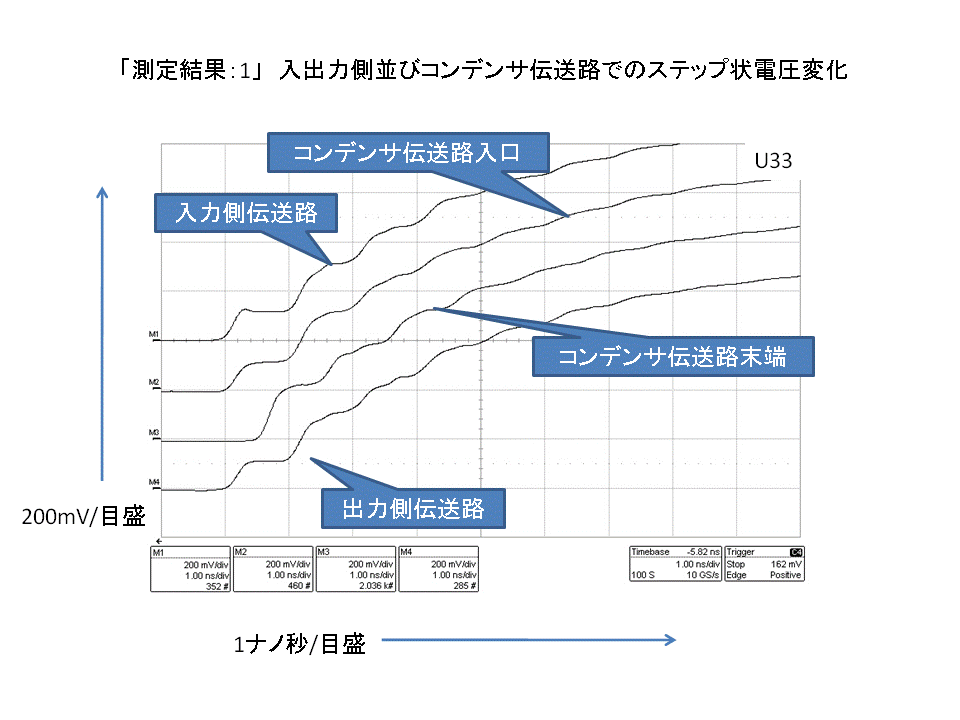 |
そして、初期のステップの低さから出力伝送路への出力は、この低いステップ状態に留まる波長の短い信号は、殆どカットされる事も分かります。
この件は、次の「測定結果:2」(コンデンサが飽和状態の場合)でも、入力信号に比較して、各伝送路で示される各々の電圧波形の立ち上がり立下りの鈍り具合からもはっきりします。
そして「測定結果:3」の入力信号オン/オフ時の同一性(上昇/下降の向きは逆)も、先の縦列接合コンデンサの場合と同じであることも分かります。
これらの点からも、従来「バイパス・コンデンサ」と言われているコンデンサも低特性インピーダンスの(並列接合された)伝送路であり、先の縦列接合された場合が“高周波信号を通し、低周波信号をカット”する役割を果たすのに対して、並列接合されたコンデンサは、逆に、“高周波信号をカットし低周波信号を通す”とコンデンサとして果たす役割に差が生じているだけである事が分かります。
このような事実を知っても「コンデンサを通して流れる電流は“変位電流”である」との説に固執するでしょうか?
では、もうひとつの事例をご覧ください。
| 「その2:直列接合されている状態のコンデンサ」 |
次の「図:3」のように、入力側伝送路へ出力側伝送路と共に直列接合されている状態のコンデンサについて考察します。
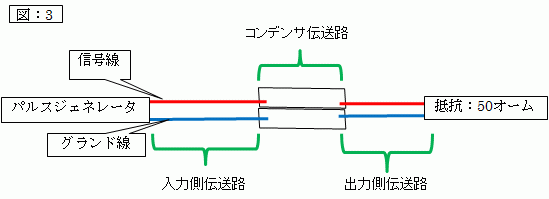 |
このようなコンデンサ伝送路(コンデンサ程に低特性インピーダンスではなくても)に対しては、「線間容量」等とコンデンサとは別扱いされています。
しかし、この状態ははっきりと「コンデンサ伝送路」である!
しかも、「直列接合されている状態のコンデンサ」である!と断言します。
そして、上に述べたバイパス・コンデンサ(並列接合されている状態のコンデンサ)と同様な働きを呈してくれるのです。
先ずは、「イメージ図:4」をご覧ください。
そして、イメージ図に付した説明書きも御覧ください。
| イメージ図:4 |
次の「イメージ図:5&6」もイメージ図に付した説明書き共々ご覧ください。
| イメージ図:5 |
| イメージ図:6 |
いかがでしょうか?
先の「並列接合されている状態のコンデンサ」と相違点は、「図:1」と「図:3」の相違のように、コンデンサ伝送路の電圧波形が立っているか横になって表示されているかだけです。
| 一般的な伝送路の反射現象に関する1点だけです。 |
|
特性インピーダンスの異なる地点では、電流の反射現象が生じます。 しかし、この反射地点のその前後の伝送路での電圧は等しくなります。 (入力電流+反射電流)×入力側伝送路の特性インピーダンス =(反射点先電流(=入力電流−反射電流))×反射点先の伝送路の特性インピーダンス |
更には、上の並列接合の場合同様に、電源(パルスジェネレータ)から、1MHz(1ボルト)のクロック信号を1パルス、出力して次の各種の測定を行いました。
次の「測定結果:4」から、並列接合の場合と同様なステップ状に電圧が変化する様子が提示されています。
(コンデンサ伝送路の末端では、他のステップより2倍ほど高くなっております)
この場合も、初期のステップの低さから出力伝送路への出力は、この低いステップ状態に留まる波長の短い信号は、殆どカットされる事も分かります。
この並列と直列の場合の類似性を、入力信号オン/オフ時の上昇/下降のステップ状変化を併せて記録したのが次の「測定結果:5」です。
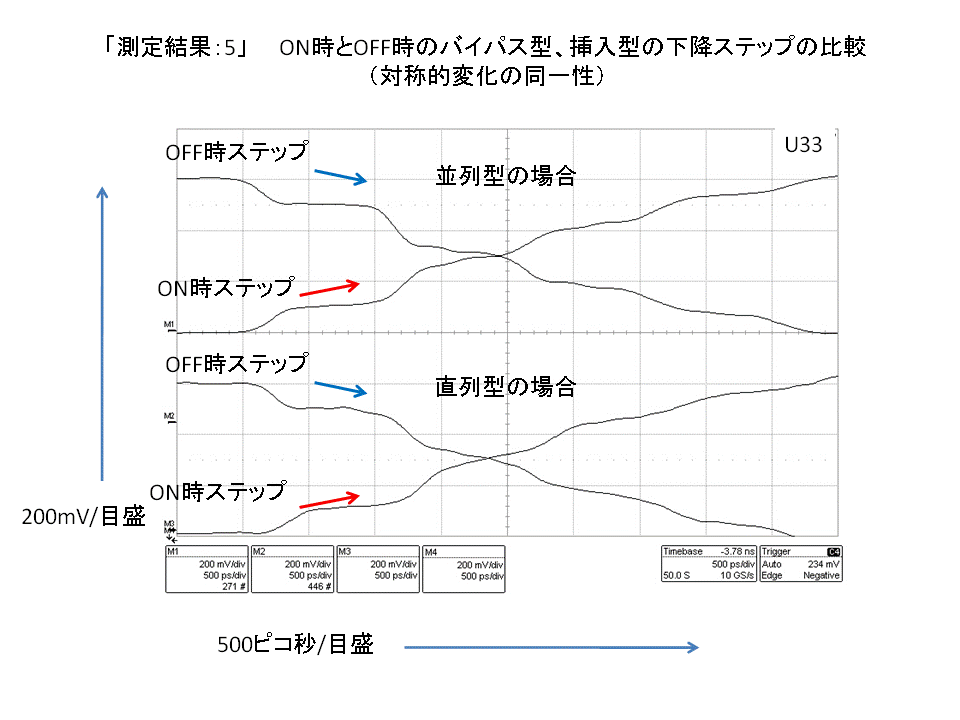 |
そして、入力信号オン/オフ時のコンデンサとしての挙動が、「並列接合コンデンサの場合」、「直列接合コンデンサの場合」も同一性(上昇/下降の向きは逆)を有しており、この傾向は、先の縦列接合コンデンサの場合と同じであることも分かります。
次の「測定結果:6」(コンデンサが飽和状態の場合)でも、並列接合の場合同様に、入力信号に比較して、各伝送路で示される各々の電圧波形の立ち上がり立下りの鈍り具合からもはっきりします。
これらの測定結果は、先に掲げた「イメージ図:4、5&6」(直列接合された低特性インピーダンス=バイパス・コンデンサ)を反映しております。
(注:次の枠内の記述は、気になる方はお読みください。でも、読み飛ばされても結構とも存じます)
|
ここで、先の並列接合の場合と、今回の場合での、入力伝送路からコンデンサ伝送路、又、コンデンサ伝送路から入出力伝送路への反射係数の相違を見て見ますと、ほとんどかわらないことがわかります。
何しろ、入力側伝送路からでは、前者が特性インピーダンスがとても小さいコンデンサ伝送路に出力伝送路が並列接合されているのですから、この場合の反射係数は、入力側伝送路とコンデンサ伝送路の間で決まります。
後者は、当然、入力側伝送路とコンデンサ伝送路の間で決まります。
次に、コンデンサ伝送路側からの反射係数ですが、並列接合の場合は、入出力伝送路の合成特性インピーダンス値はそれらの1/2となり小さくなります。
一方、直列接合の場合は、そのままの値ですから、反射係数自体も並列接合の場合の約2倍となる為、入出力伝送路へ流れだす電流量は並列接合の場合の1/2となってしまいます。
ところが、並列接合の場合はコンデンサの入口部のみの反射ですが、直列接合の場合は両側で発生しますから、コンデンサ伝送路内の電流が1往復間に両伝送路へ流れだす量は2倍となり、結局は並列接合、直列接合の場合とも今回の測定結果のように同様な結果に落ち着くのです。 |
この「図:3」に示されたように、入出力伝送路間に「直列接合されたコンデンサ」に対して、“コンデンサを通して流れる電流は「変位電流」である”との理論を振りかざしたところで、無意味である事は明々白々です。
従いまして、先の≪敬愛するマイケル・ファラデー(7) 縦列接合がコンデンサの謎を解く≫と今回の考察から、コンデンサに関しては次の結論に落ち着くと存じます。
即ち、
|
コンデンサは、 「電荷を溜める」魔法の玉手箱のような存在ではなく、 又、コンデンサを通して流れる電流は“変位電流”でもなく、 コンデンサは、 低特性インピーダンスの伝送路であって、 接続方法(縦列接合、並列接合、直列接合)の相違に伴う反射現象の変化から、 |
そして、重ねて書かせて下さい。
| 此処までで検証されてきた、上述のコンデンサ理論の正当性から、 不肖、私の発見たる「縦列接合」も世間に認知される正当な根拠を得る事となります。 |
くどいようですがもう一度書きましょう。
このような事実を知っても「コンデンサを通して流れる電流は“変位電流”である」との説に固執するでしょうか?
(補足:1)
線間容量(並びにコンデンサの容量)
世の中には「線間容量」と言う言葉が流布しているようですが、ここでの「容量」との言葉は、いわゆる「コンデンサの電極間に電荷が蓄えられる」同様に、「2本(3相の場合は3本)からなる電線間に電荷が蓄えられる」の発想から発生してきたのでしょう。
しかし、今回の直列接合されたコンデンサからお分かり頂けますように、特性インピーダンスがコンデンサ伝送路ほど低くはなくても一定値の値を示す(注)同軸ケーブルや、並行線などの両端に接続される配線のそれが大きかったり、そこに大きな値の抵抗がセットされていたら、これら同軸ケーブルは、先に示した直列接合されたコンデンサ同様な振る舞いを示すでしょう。
(注:伝送路内の特性インピーダンスの値がばらついている場合には、その伝送路内で多重反射が生じて、対象となる伝送路の両端での反射現象は明確にならなくなります。
この件は、後に触れられたら触れようと思っております)
ですから、「線間容量」と言う言葉も「俗説」となって頂かなくてはならないのです。
尚、直列接合コンデンサ(勿論、縦列、並列接合のコンデンサ)から分かりますように、コンデンサの挙動は、入出力側の伝送路とコンデンサ伝送路の特性インピーダンスの相違による反射現象が支配しているのですから、コンデンサの容量(或いは線間容量)を求める場合には、測定(計算)対象の伝送路の特性インピーダンスもさることながら、入出力側の伝送路の特性インピーダンス(低周波数の信号を扱う場合には、伝送路の特性インピーダンス値よりも入出力伝送路中にセットされた抵抗値)が問題となってきます。
(補足:2)
“コンデンサは伝送路である”と、私は、10年ほど前から、日本のパソコンメーカーの基板設計製造担当者らの定期的な会合に於いて訴え続けてきました。
しかし、彼らは私の説を全面的に理解してはくれませんでした。
ですから、彼らの所属する会社からの自著『コロンブスの電磁気学』並びに『コロンブスの電磁気学』増補改訂版の大量発注を私は今もって得る事が出来ません。
(私は大いに期待していたのですが!)
そんな中、「Ivor Catt氏著 "Electromagnetics 1", Westfield
Press, 1995のPrefaceページviiiに“a capacitor was in fact a transmission line.(コンデンサは伝送路である)”と記述されている」との情報を得ましたので、「コンデンサは伝送路である」と公に唱えたのは、私が最初ではないことになります。
勿論、流石のIvor Catt氏といえども「縦列接合の発見」等までには目が届いて居られなかったようですが、正直ちょっと残念でした。
それにしても、私の件はさておきましてもIvor Catt氏の提唱以来、15年も経過しても、依然として、世間は「コンデンサは電荷を蓄える論」を信じ込んでいます。
そこで、テレビやインターネットなどで、「俗説」に果敢に挑まれる早稲田大学名誉教授の大槻義彦氏が編者のお1人である『新・物理学事典(講談社:2009年6月20日第1刷発行、同年7月16日第2刷発行)』の第2刷を購入し、パラパラと頁をめくってみました。
しかし、残念ながら「コンデンサは電荷を蓄え、コイルは磁界を蓄える」的な論に終始していました。
ところが、Ivor Catt氏も入手出来なかった「縦列接合と言う魔法の鍵」をしっかりと握りしめた私は、“コイルも縦列接合された伝送路である”等々の証明も行っているのです。
ですから、次の≪敬愛するマイケル・ファラデー(9) 縦列接合がコイルの謎を解く≫に移らせて頂きたく存じます。