「こんなことでよいのでしょうか？」の目次へ戻る 「我が科学の世界」の目次へ戻る 『コロンブスの電磁気学』の概略へ 『コロンブスの電磁気学』増補改訂版の概略へ

『コロンブスの電磁気学』増補改訂版（A4判　831頁　価格：6000円） ご購入ご希望の方は、ご住所ご氏名をご連絡下さい。 送料当方負担にて送らせて頂きます

敬愛するマイケル・ファラデー（7）　縦列接合がコンデンサの謎を解く

2011年2月6日

宇佐美　保

 

　先の拙文≪敬愛するマイケル・ファラデー（5）　縦列接合の登場≫にて紹介させて頂いた「縦列接合の発見」によって、「電流とは電荷の移動である」との従来説から、新たな「電流は、電磁波川の流れと導体堤防間の相互作用」説（この件は）前文の≪敬愛するマイケル・ファラデー（6）　縦列接合された伝送路に流れる電流値は同一である≫もご参照ください）への移行を可能にし、且つ、その結果、新たな視野が開けてきます。

 

　この新しい視点から、先ずコンデンサ理論を見直してみます。

（詳細は、自著『コロンブスの電磁気学』増補改訂版をご参照ください。

そこでは、コンデンサに関する新たな理論形成に関して、各種の傍証検証を141頁にわたって行っております）

 

　私達は今までコンデンサ（キャパシター）は、「2枚の電極とその間を絶縁する層（誘電体層）で構成される電荷を蓄える素子（電気部品）」と教わって来ました。

 

　しかし、コンデンサの電極間が絶縁されているのに、このコンデンサを通して「電荷の移動である電流」（直流はともかく（特に周波数の高い）交流）が流れる理屈が分かりませんでしたが、Ｊ. Ｃマクスウェルは「変位電流」を提起してこの問題を（従来までは）解決して来ました。

 

「変位電流の概略」

 

電源のプラス側から流れて来たプラス電荷は、電線を伝わりその電線に接続している方の電極には到達できますが、絶縁されている他方の電極へは移動できません。

そこで接続している側の電極にそのプラス電荷は蓄えられるでしょう。

その結果、その電極の電位は、他方の電極の電位より高くなり、その電位の時間的変化に比例して、絶縁されている他方の電極側へも「変位電流」なる電流が流れるとマクスウェルは考えたのだと存じます。

 

　そこで、この電源電圧をＶボルトとして、電線にセットされている抵抗の値をＲオームとしますと、コンデンサ内電圧（Ｖ）の時間的変化式として次式が求められています。

 

 

 

この式に従って、コンデンサ内の電圧（V）の時間的電圧変化は、次のような概念図（図：1）を描く事が可能です。

 

 

　しかし、次のような測定をしてみますと、マクスウェルの唱えた「変位電流説」を逸脱する結果が得られます。

　

　接着剤付き銅箔（厚さ：0.035mm）を幅：10mmに切断し、これをセロテープの両面に貼り付けて、「写真：1」の3種類のコンデンサ（各長さ:10cm、20cm、30cm）を作成して、これらの「コンデンサ」の内部（入口部）電圧変化を「写真:２」のようにして、電源であるパルスジェネレータから、特性インピーダンスが50オームの伝送路を通して、銅箔伝送路へ1パルスのクロック信号（周波数：1ＫHz、出力：500mV）を入力し、差動プローブを用いて測定し「測定結果：１」を得ましました。

 

（「写真：2」の状態では、電源のプラス端子は銅箔テープ伝送路の一方の電極へ接続され、他方の電極はマイナス端子に接続されている事になります。

そして、この電源の内部抵抗は50オームである事は言うまでもありません）

 

 

 

尚、伝送路の電圧変化の立上り（上昇部分）と立下り（下降部分）を上昇開始時、下降開始時の変化部分を拡大し、且つ、それらの開始位置を合わせて表示しました。

 

　この結果から明らかなように、コンデンサ内の電圧変化は段階的であります。

そして、その段階的変化のインターバルは、コンデンサを構成する銅箔長に比例して大きくなります。

 

この上昇時と下降時とに示される同一な周期性を有する段階的変化のインターバル（ステップ長）とコンデンサの長さの関係を次の「表：1」に纏めます。

 

 

　この結果から、電流（電磁波流）がコンデンサの入口と末端間を、約20cm/ナノ秒の速度で往復していると推測する事が可能です。

 

　このような現象はとても先の「変位電流説」から導かれた「式：1」では表現不可能です。

従って、この時点で「変位電流説」を破棄しなくてはならないのですが、しかし、もう少し、その破棄すべき根拠を別の測定結果から提示します。

　即ち、次の「図：2」のようにパルスジェネレータ（1ボルト、1MHzの1パルスのクロック信号を出力）、銅箔コンデンサ（幅：5、長さ：10cm）、抵抗を同軸ケーブルで結び、各部での電圧変化を差動プローブにて「測定結果：2」を得ました。

 

 

 

　このように、ステップは入口部、又、末端部でも同様に観測されます。

（但し、入口部での最初のステップの高さ（約60mV）は、末端部での最初のステップ高さ（約120mV）の半分しかありません）

しかし、入口部と末端部でのステップ位置は、約500ピコ秒（約1/2ナノ秒）の時間差があります。

この時間は、先の「測定結果：1」の場合同様に、電磁波が約20cm/ナノ秒の速度で、この銅箔コンデンサ（セロテープ中）の入口部から10cm離れた末端部へ進行する時間に相当すると考えられます。

 

　更には、コンデンサ入口部、入力側の伝路並びに出力側の伝送路に於ける電圧変化を測定しますと、次の「測定結果：3」を得る事が出来ます。

 

 

 

　この結果を見るように、コンデンサ入口部、出力側の伝送路に於ける電圧変化波形は、従来説でも納得できますが、入力側の伝送路へも当初の入力波形（1ボルト）に加えて、更なる1ボルト（ピーク時）の電圧波形が認められるのです。

 

この点をよりはっきりと確認する（パルスジェネレータからの当初の入力信号と、コンデンサ部からの反射波を分離して確認する）為に、入出力用の同軸ケーブルの長さを10メートル（「測定結果：2」の場合は各1メートル）とし、且つ、入力する信号の信号保持時間を短くする為、周波数を、先の1MHzよりも、50ＭＨｚとより高周波の信号をパルスジェネレータから出力し、パルスジェネレータ出力端子直前（並びに、出力側のケーブルの末端部）での測定結果を次の「測定結果：4」に掲げます。

 

 

　
　この結果からもコンデンサを通して出力側の伝送路へ電流が流れていると共に、入力側へも流れている事が、はっきりと再確認出来ます。

 

　更に、先の「測定結果：3」から次の結果「測定結果：5」も得られます。

 

 

 

　即ち、コンデンサ内電圧波形の1/2が、入力伝送路を逆流する電圧波形とほぼ合致する事が分かるのです。

 

　このような現象も従来の「変位電流がコンデンサを通して流れる」説から解説されておりません。

（但し、電気は（単独で）プラスからマイナス方向だけでなく、別に、マイナスからプラス方向にも流れ、且つ、「変位電流」を “電位の変化のマイナス側にはマイナス電流、プラス側にはプラス電流がその変化に比例して流れる”と 拡張解釈すると今回の測定結果もある程度は説明出来ますが、一般的な回路（シングルエンド的な流れを想定した回路）では、1本の電線を伝わって、プラスマイナスの電気が逆方向からコンデンサの位置まで到達するにはジャンの時間的ずれも生じます。

以上の件は、さておきまして、先の段階的な電圧変化は「変位電流説」では説明できません）

 

 

　更に次に進む前に、「測定結果：6」も御覧ください。

 

この場合も「測定結果：1」と同様なオン/オフ時対称的なステップ状変化が得られております。

 

 

　このように従来の「変位電流説」では説明に窮する現象も、「縦列接合の発見」の恩恵に浴して頂ければすぐに解決するのです。

 

即ち、コンデンサは、入力側並び出力側の伝送路に縦列接合された伝送路（但し、その特性インピーダンスの値が小さい）と、又、併せて、電流は電磁波川の流れと導体堤防間の相互作用であると認識する事で、今回の測定結果を容易に解釈する事が可能となるのです。（先の≪敬愛するマイケル・ファラデー（6）　縦列接合された伝送路に流れる電流値は同一である≫をご参照ください）

 

先ずは、この状況を、先の十字型に縦列された伝送路からコンデンサ伝送路への次のイメージ図をご参照ください。

 

 

 

　このコンデンサ伝送路と出力伝送路が入力伝送路に縦列接合されている状態で、入力伝送路側からクロック信号が入力された場合の各伝送路での電流（電磁波川の流れと導体堤防間の相互作用）の流れ具合のイメージ図をご覧ください。

 

先ず「イメージ図：1」ですが、ここでは、入力側並びに出力側の伝送路の特性インピーダンスが等しくZであり、コンデンサ伝送路のそれがZ_c（但し、Z≫Z_c）とすると、入力伝送路から流れて来た電流は、僅かに反射して戻りますが、残りの電流は、コンデンサ伝送路と出力側の伝送路に、そのままその量を変えることなく等しく流れ込んで行きます。

そして、「測定結果：2」のコンデンサ入口部の最初のステップ電圧波形が観測されます。

 

 

 

　次の「イメージ図：2」は、出力側の伝送路は電流が流れ続けていますが、コンデンサ伝送路ではその末端まで進行した電流は完全反射され入口部へ戻って行きます。

 

この時、「測定結果：2」に見ますように、先の入力部のステップ電圧波形の出現から、電磁波がコンデンサ伝送路の片道を進行する時間遅れて、先のステップの2倍の電圧が末端部で観測されます。

 

　「イメージ図：3」では、末端部から入口部に戻って来た電流は、その一部を入力出力側の伝送路に排出しながら、又、瞬時に末端へと進行して行きます。

この時、「測定結果：2」に見ますように、コンデンサ入口部のステップ波形は、当初の2倍弱の増大を示します。

 

この際、（コンデンサ伝送路内の電磁波の流れが末端で完全反射を受けて入口部へ戻ってくることから）当然ながら、入力側の伝送路へはプラス電流が排出されていますが、（入口に戻ってくる電磁波の色でお分かり頂けますように）出力側の伝送路へはマイナス電流を排出されている点に注目して頂きたいのです。

 

 

但し以降のイメージ図では、若干省略して表記します。

例えば、「イメージ図：3」の省略イメージ図への移り変わりを次に示します。

 

 

　

　ここで、少し数式を使った説明を補足しますが、数式のお嫌いな方は、次に掲げます重要な3項目を頭の中にお入れになって、式の部分は目をつぶってお読みください。

（又、ここでの記述では不十分なお方は自著『コロンブスの電磁気学』増補改訂版をご参照ください）

 

先ずは、

一般的な伝送路の反射現象に関する1点
第1項	特性インピーダンスの異なる地点では、電流の反射現象が生じます。 しかし、この反射地点のその前後の伝送路での電圧は等しくなります。 （入力電流+反射電流）×入力側伝送路の特性インピーダンス ＝（反射点先電流（＝入力電流−反射電流））×反射点先の伝送路の特性インピーダンス

　次は、

「縦列接合」に関する私の見解の2点
第2項	縦列接合された伝送路の合成特性インピーダンスは、それぞれの伝送路の特性インピ　ーダンスの和となります。 （前の≪敬愛するマイケル・ファラデー（6）　縦列接合された伝送路に流れる電流値は同一である≫からも、 ある程度は御推測可能と存じます）
第3項	縦列接合では、縦列された伝送路には、同一値の電流が流れる。

 

「数式による考察」

 

　以下に於いて、今回の場合では、上記の第2項に於ける、入力伝送路側（入力伝送路）からの反射点先の伝送路は、縦列接合された出力伝送路とコンデンサ伝送路と言う事になり、又、コンデンサ伝送路側からの反射点先の伝送路は、縦列接合された入力伝送路と出力伝送路と言う事になります。

 

　上に掲げた第2項を参照して、入力伝送路（Z）の、縦列接合された出力伝送路（Z）とコンデンサ伝送路（Z_c）からの反射係数（τ）は、次の式を見て分かりますように、随分小さな値です。（∵Z≫Z_c）

 

 　　

 

　

（この式は参考にとどめて目をつぶっても良いのですが）

入力側の伝送路からVボルト、即ち、i＝V/Zアンペアの電流が入力されますと、僅かな電流（τi）が入力電源側に反射され戻って行き、大部分である残りの電流（i（1−τ））が出力側の伝送路、並びに、コンデンサ側の伝送路へと等しく流れ込みます。

 

　ここで、上記の第1項の「反射地点のその前後の伝送路での電圧は等しくなります。

（入力電流+反射電流）×入力側伝送路の特性インピーダンス ＝（進行電流（＝入力電流−反射電流））×進行先の伝送路の特性インピーダンス」

を活用させて頂きますと、

i（1+τ）Z＝i（1−τ）（Z+Z_c）

この式を少し変形します。

i（1−τ）Z+2iτZ＝i（1−τ）Z+i（1-τ）Z_c（式：2）

 

　ここで、右辺の第1項：i（1−τ）Zは出力側の進行電流に起因する電圧であり、左辺の第1項と同じとなります。

となりますと、

2iτZ＝i（1−τ）Z　　（式：3）

が残ります。

　ここで、この右辺は、コンデンサ伝送路に入り込んだ進行電流によるコンデンサ伝送路内の電圧です。

そして、左辺のiτZは、入力側伝送路の反射電流による入力伝送路側の電圧です。

　従って、

コンデンサ伝送路内に入り込んだ進行電流による電圧 ＝（反射電流による入力伝送路側の電圧）×2 （＝（反射電流による出力伝送路側の電圧）×2）

（式：4）

　　

と言う事が分かります。

 

　一方、コンデンサ伝送路（Z_c）に対して、縦列接合された入力側伝送路（Z）並び出力側伝送路（Z）とからの反射係数（τ_c）は、次のようにほぼ1に近いのですが、1より若干小さな値である事が分かります。

（∵Z≫Z_c）

　

　

（この式も参考にとどめて目をつぶっても良いのですが）

 

　コンデンサ伝送路内電流（i_c）が、縦列接合分岐点に着ますと、この反射係数（τ_c）に従っての反射現象が発生します。

 

　ここで、又、

第1項の「反射地点のその前後の伝送路での電圧は等しくなります。

（入力電流+反射電流）×入力側伝送路の特性インピーダンス ＝（進行電流（＝入力電流−反射電流））×進行先の伝送路の特性インピーダンス」

を活用させて頂きますと、

i_c（1+τ_c）Z_c＝i_c（1−τ_c）（Z+Z）

この式を少し変形します。

 

i_c Z_c + i_cτ_cZ_c＝i_c（1−τ_c）Z+ i_c（1−τ_c）Z　　　（式：6）

 

　この式の意味は、次のように表す事が出来ます。

コンデンサ伝送路の入口部に到達した電流とその反射電流分によるコンデンサ内電圧 ＝（入力伝送路側に流れ込む電流による電圧）×2 （＝（出力伝送路側に流れ込む電流による電圧）×2）

（式：7）

 

 

　これらの状態は、入力信号がこの縦列接合点（コンデンサ入口部）迄、流れてくる間続きます。

これらの電流を、先の「イメージ図：1〜3」のように、赤系青系の色をしたリボンに見立てて頂くと次からの説明が御理解し易いと存じます。

と申しますのは、≪『コロンブスの電磁気学』増補改訂版の概略≫の「3　電気の流れ　（電気は、近接作用です）」に於ける「測定結果：3」に見ますように、伝送路の末端まで行って帰ってくる電流とこれから末端へ行く電流が途中でぶつかり合う事態となっても、水の流れのように両者が合体してしまったりする事態は発生せず、お互いそれぞれの形を有したまま進行するのですから、電流のイメージとしては「水の流れ」よりも「リボン」とする方がこれから先を理解するのに便利かと存じますので。

 

　ですから、電源から入力伝送路へ「i」の幅で供給されたリボンが、縦列接合分岐路で、反射係数（τ）分引き裂かれて元来た道をiτ幅のリボンが戻り、その残り（1-τ）分の幅を有したリボンが、出力側伝送路並びコンデンサ伝送路へと、進行するイメージなのです。

 

但し、ここで注意しなくてはならないのは、縦列接合された伝送路の特徴として、（上記にても掲げましたが）この残りの（1-τ）分が出力側の伝送路並びコンデンサ伝送路へ2分割されて進行するのではなく、両者に等しく（1-τ）分が流入して行くのです。

この様子が先の「イメージ図：1」に相当します。

 

即ち、その幅を維持したまま引き裂かれることなく（その幅のまま上下2枚のリボンに剥離されたと如く）両伝送路へと流れて行くのです。

 

　次の展開は先に記述しましたが、「イメージ図：3」では、コンデンサ伝送路を往復して入口部に戻って来たリボンが、コンデンサ伝送路側からの反射係数（τc）分と、残りの（1-τ_c）分とに割かれ、この残りのリボンは先と同様にその幅が再分割されることなく等しく入力側並び出力側の伝送路へと進行して行きます。

 

　そして、

留意しなくてはいけないのは、リボンが引き裂かれるのは、コンデンサの入口部に於いてだけなのです。 譬えてみれば、コンデンサの入口だけにリボンを引き裂くナイフが設置されているような状態です。 ですから、リボンの幅が変化するのは入口部だけで、入口部以外ではリボンの幅は変化しないのです。 そして、この結果、コンデンサと各伝送路の電圧変化は、 このリボンの先頭がコンデンサ伝送路を往復して入口部へ戻ってくる毎に、しかもステップ状でしか発生しないのです。 （勿論、その間、往復回数に応じて幅をステップ状引き裂かれた後続リボンの各所は、 その間も入口部へ戻ってきては、入口部のナイフで引き裂かれ続けているのです、 即ち、リボンの引き裂き減少は常時発生しているのです）

 

　このコンデンサ伝送路の往復をn回繰り返し、再度コンデンサ伝送路の末端へと逆行して行くリボンの幅は、（τ_c）ⁿ　とに減じて行くでしょう。

 

　一方、コンデンサ伝送路から排出されて、入力並びに出力伝送路へ向かうリボンの幅も、往復をn回時点では、（1-τ_c）ⁿ　に狭まって行きます。

 

　この状態を、次のイメージ図で示します。

但し今回は、作図の関係上（図を見て頂けばお分かりのように）入出力側の伝送路に於いては、時間単位をコンデンサ伝送路のそれより狭め、又、グランド線側の変化を省略して、信号線側のみを図示しました。

 

そして、「イメージ図：4」から、「イメージ図：5」、更には、「イメージ図：6」のような飽和状態となります。

 

（尚、これらのイメージ図の「白地で緑枠の部分」は、先の「「イメージ図：3」の省略イメージ図への移り変わり」に見ますように、「プラス/マイナスの電流が相殺し合って」、見かけ上電流がゼロとなって見えるのであって、その裏には、絶対値が等しいプラス並びマイナスの電流が流れているのです）

 

 

　これらの様相の変化を次のアニメーションでご覧下さいコンデンサ入力時の変化に関するアニメーション。

 

 

 

　

 

先ずは「イメージ図：7」の如く、入力側の伝送路への反射波はなくなります。

そして、入力伝送路からの出力側の伝送路へ、又、コンデンサ伝送路への信号の流入も途絶えます。

 

 

 

　それでも、コンデンサ伝送路内で反射を繰り返している電流からは、入出力側の伝送路への電流の排出はしばらく続きます。

ところが、「イメージ図：8」のように、新たにコンデンサ伝送路への流入は途絶えていますから、反射回数が0回目、1回目、2回目と反射回数の少ない電流からどんどん（しっぽを切られるように）消滅して行きます。

 

　そして最後は、「イメージ図：9」のように、コンデンサ伝送路内の電流もすべて消滅して、入出力側の伝送路への電流の排出も完全になくなります。

 

　これらの様相の変化を次のアニメーションでご覧下さい。

 

 

　尚、ここまでのイメージ図から、実際の観測波形（「測定結果：1〜6」）との比較を行います。

 

　先ずは、電圧測定器（オシロスコープ）での「入力側の伝送路での観測波形」と「出力側の伝送路での観測波形」と、今回のイメージ図を比較します。

 

但し、オシロスコープの表示画面との合致性を容易に確認できるように、「入力側の伝送路での観測波形」のイメージ図では、入力オフ後の電圧変化は電圧積立順序を逆転しています。

更に、「出力側の伝送路での観測波形」のイメージ図では、時間軸方向を反転しています。

 

　この「イメージ図：10」は、先に掲げた「測定結果：3」と同様な電圧変化形状を示しています。

 

 

　次の「イメージ図：11」は「測定結果：5」に対する検討として掲げました。

 

　此処に於いて、「コンデンサ入口部」の波形も「入力側への逆行分」の波形の2倍の形と見なせます。
（但し、実際の電圧値に関しては、後に数式から考察いたします）

 

　但し、以上の考察は、入力信号がオンされた時、即ち、飽和状態へと立ち上がって行く過程の波形に関しての考察です。

 

　そこで、入力信号がオフされた時、即ち、飽和状態から、立ち下がって行く場合の波形変化も加えた、次の「イメージ図：12」で考察しましょう。

 

 

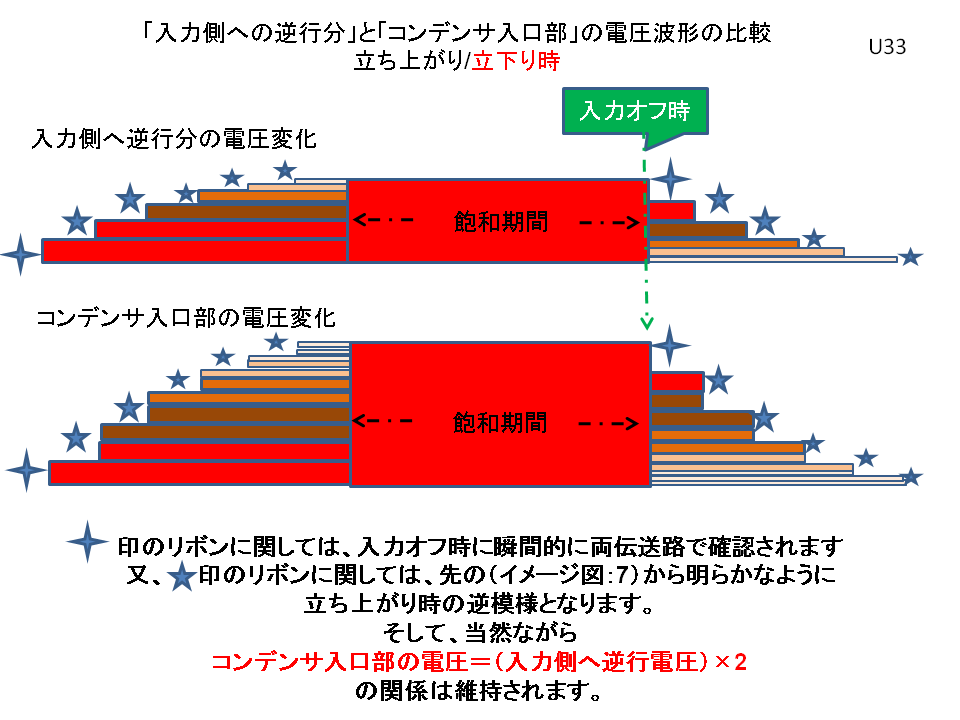　この結果は、「測定結果：6」のように、立ち上がり時立下り時の段階的変化を比較しますと、両者は上下全く対照的な関係にある事が分かります。

 

　即ち、「測定結果：5」に対して、このようなイメージ図並び計算等を用いた考察が合致するのです。

更には、次の「測定結果：7」もご覧ください。

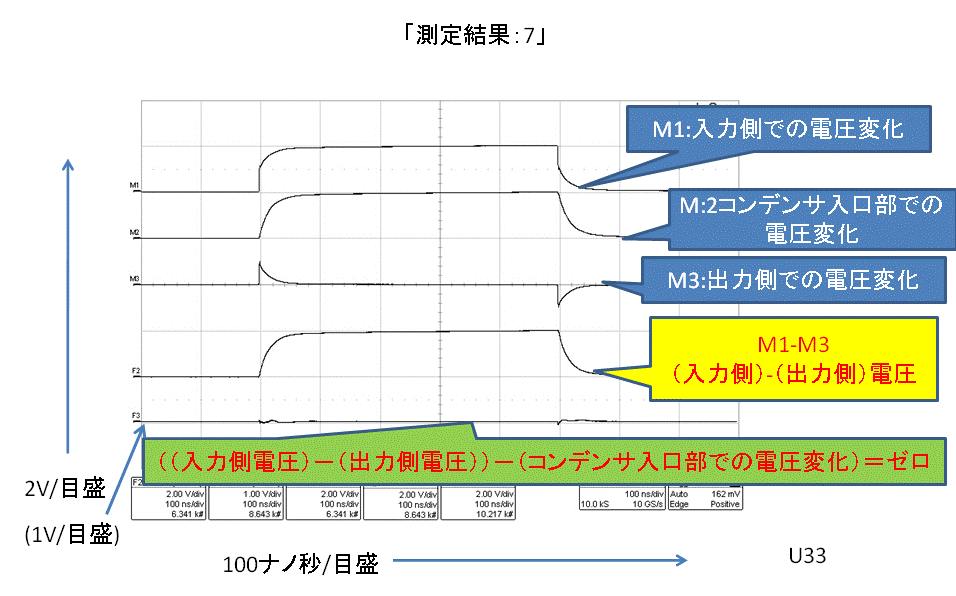　この結果からお分かり頂きますように、（「入力側の伝送路で検出される電圧変化」マイナス「出力側の伝送路で検出される電圧変化」）が「コンデンサ入口部で検出される電圧変化」とが等しい関係にある事が分かります。

　この根拠は、先に掲げた「3項目」である事は言うまでもありません。

但し、念のために、次の3点を書き添えさせて頂きますと、

「出力側の伝送路で検出される電圧変化」は、出力側の信号線が、コンデンサ伝送路のグランド線とつながっている為に、 「入力側の伝送路で検出される電圧変化」に加算する「出力側の伝送路で検出される電圧変化」としては、 オシロスコープで観測された「出力側の伝送路で検出される電圧変化」にマイナス符号をつける必要があるからです。

　更には、「イメージ図：1」を御覧下されば御納得頂けると存じますが、

「出力側伝送路へ進む電流（電圧）」＝「入力側伝送路を進んできた入力電流（電圧）」マイナス「入力側への反射電流（電圧）」 ∴　「入力側の伝送路で検出される電圧変化」マイナス「出力側の伝送路で検出される電圧変化」＝「入力側への反射電流（電圧）」×2

　もう1点付けくわえさせて頂きますと（先にも提示しましたが）、

コンデンサ伝送路入口部での反射現象によって生じる、 「コンデンサ内部の電圧変化」＝「入力伝送路での電圧変化」+「-（出力伝送路での電圧変化）」 の関係が成り立ちます。

以上の各種考察から、
　

”「図：2」のように 信号線内にセットされたコンデンサが、 入力側の伝送路に対して、出力側の伝送路と共に縦列接合された伝送路である” との証明が可能となるのです。

 

（補足）

 

先の≪敬愛するマイケル・ファラデー（5）　縦列接合の登場≫の、（「縦列接合」を御納得頂く為の補足実験）に於いて、入力側から3本（縦列接合されて）に分岐したスピーカーコードの1本のみの末端電圧をテスターで測定すると、家庭用の1ボルト交流（50ヘルツ）入力時では、どの末端に於いても9ボルトが検出されたのに、乾電池（直流）による入力時には、どの末端とも電圧が検出されなかったのは、測定したその1本のスピーカーコードがコンデンサとして振る舞ったからでありましょう。

（∵　テスターの測定時の内部抵抗は10メガオームでしたから、テスターで測定したスピーカーコードは、末端に10メガオームの抵抗がセットされた出力伝送路との挙動を示した事となります）

 

　そして、3本同時に3個のテスターを用いて測定した場合には、その3本のスピーカーコードが出力伝送路となり、コンデンサが存在しなくなるから、各出力端の検出電圧は等しく、又それらの和が入力電圧と等しくなると考えられます。

（又、別の考えをしますと、3本のスピーカーコードコンデンサの末端に等しい値の抵抗が設置されたので（出力伝送路が存在しなくなり）、各コンデンサ間また、入力伝送路との電流のやり取りも平衡に達した結果とも考えられます）

 

　この稿は余り長くなりましたので、次の≪敬愛するマイケル・ファラデー（8）　縦列接合以外のコンデンサ≫に移らせて頂きたく存じます。