|
『コロンブスの電磁気学』増補改訂版(A4判 831頁 価格:6000円) |
敬愛するマイケル・ファラデー(5) 縦列接合の登場
2011年1月18日
宇佐美 保
前の拙文≪敬愛するマイケル・ファラデー(4) ファラデーの無念が今まで晴らせなかった理由≫迄で、ファラデーの当初の予想(電池につないだ電線に流れる電流と同様な電流が検流計につないだ電線にも流れる筈だ!)の正当性を証明して来ました。
それでも、従来の「電磁誘導説」に固執して、受動伝送路に誘起される電気信号は、能動伝送路の信号がオンオフした時のみであるべきだ!との思いを捨てきれないお方は、どうか、アンテナの事を思い浮かべてほしいのです。
何しろ、私達は日常生活で、送信アンテナに送り込まれる電流(電気信号)が、そのアンテナから電磁波(電波)として空気中に発散され、その電磁波(電波)を、そっくりそのまま携帯電話などの受信アンテナで受け取り、その電磁波を電流に変える操作もしていないのに、誠に自然に電流(電気信号)として、携帯電話内部に取り込まれているのですから!
更に、このアンテナに於いても、送り出し、又、受け取る電気信号の周波数と、そのアンテナの長さには、ある関係が存在します。
(聴衆は信号をやり取りするアンテナはその分長くなります、ですから長時間流れ続ける直流をやり取りするアンテナはその長さの制限から不可能となります)
この件は、前拙文≪敬愛するマイケル・ファラデー(4)≫の於いて、長さが1メートルの能動受動伝送路間を、同じ波形の75MHzの連続クロック信号が流れた点と類似しています。
(但し、自著『コロンブスの電磁気学』増補改訂版(第17章新しいアンテナ理論の確立)をご参照頂きたいのですが、このアンテナの場合と、今回検討してきた2本の電線とでは、「電磁波のやり取り」に若干の相違があります)
このように一寸した「コロンブスの卵」的な発想の転換をして頂ければ、「電流は、導体中のプラス電荷並びマイナス電荷(電子)の流れである」と頑なに信じて居られる方も、直ぐ納得して頂けると存じます。
更に、「電流は電磁波で運ばれる」との発想転換を行いますと、偉大なファラデーでも気が付かなかったであろう(そして、不肖私が発見した)電気の現象(理論)を紹介させて頂ける事となるのです。
先ずは、縦列接合の発見なのです。
従来から、電気的な接合には、「直列(series)接合」、「並列(parallel)接合」の存在が知られておりますが、今、新たに「縦列(pile)接合」(勿論、私の独断的命名ですが、「図:1&2」等をご参照ください)の存在を宣言し、その存在理由を解き明かして行きます。
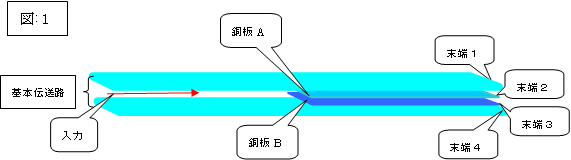
先ずは、次の「図:1」のような伝送路系を銅板で製作し、測定しました。
即ち、基本伝送路の層間に、銅板2枚を等間隔に挿入しました。
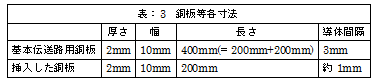
その伝送路系の各寸法を「表:1」に掲げます。
 |
 |
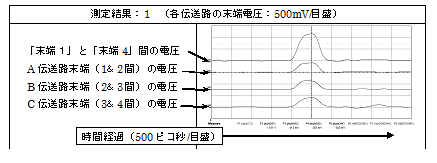
この基本伝送路に、電源(パルスジェネレータ)より1GHzのクロック信号(500mV)の1パルスを入力し、各末端(1〜4)間の電圧変化を差動プローブで測定しました。
(尚、これらの伝送路を図の上からA伝送路、B伝送路、C伝送路と呼称します)
 |
(注)
測定した各伝送路の末端はオープン状態です。
(各末端での電圧測定は、差動プローブで行いましたが、このプローブの端子間の抵抗値は1Mオームと高抵抗ですから、差動プローブをその伝送路の末端に接触させても、ほぼ完全に近い反射が生じています。)
従って、各伝送路末端での測定電圧は、伝送路を流れてくる電圧の2倍の値に観測されています。
このように、銅板A&Bのどちらも、基本伝送路に機械的に接触していないにもかかわらず、この2枚の銅板のいずれか、又、両方を有する伝送路(A、B、C)の末端には、基本伝送路とほぼ同様な電圧波形が(同時刻に)観測されているのです。
このことから、銅板A&Bを有する伝送路では、電気は電子の移動によって運ばれたのではなく電磁波の移動で運ばれたのだ!と言う事が明確になります。
特に「電荷の直接的な供給が何処からも無いB伝送路にも電流が流れる」との事実から、そして、先に記述しましたアンテナの例からして、電気は電荷ではなく電磁波で運ばれると言うことも明白となります。
以下この「縦列接合」(例えば「図:1」から説明します縦方向に重なった(接合された)伝送路、更に、それが縦方向だけでなく更に発展した接合状態)の存在を証明します。
ですから、この伝送路系(又、次のイメージ図)のように、伝送路を形成する各導体のいずれかが、基本伝送路に機械的に接触していない電気的接合を、先に宣言しましたように「縦列接合」と命名したいのです。
そして、電気の流れ(電流)は、「電荷の移動」ではなくて、「導体によって導かれる電磁波の流れ」(この流れを以後、電磁波川の流れ、導体を導体堤防と仮称させて頂きます)なのです。
一方、通常の川は土手との互いに及ぼす圧力を均衡させることで、氾濫せずに、土手に沿って流れて行きます。
そして、電磁波川の流れの場合も、導体堤防と電磁波川とが常に電気的な影響力の均衡を図ることで、導体に沿って電磁波が流れて行くのではないでしょうか?
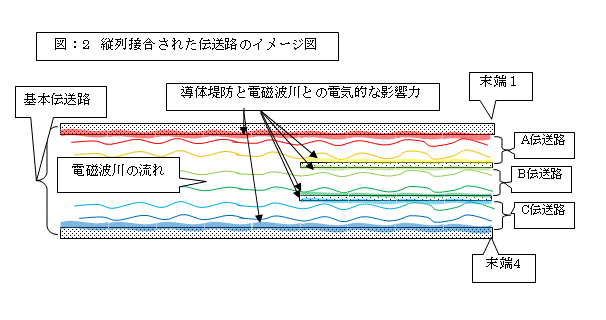
次の「図:2」は、この見解を基にした「縦列接合された伝送路」のイメージ図です。更に、基本伝送路での電磁波川の流れに関するアニメーションも御参考下さい。
(この図での導体近傍の幅の広い波模様は「導体堤防と電磁波川との電気的な影響力」をイメージして居ります)
 |
 |
更に、この縦列接合を展開いたします。
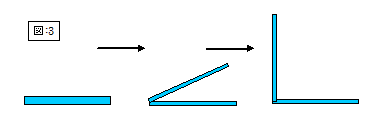
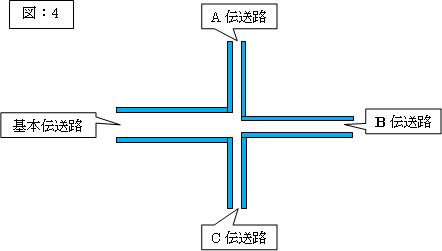
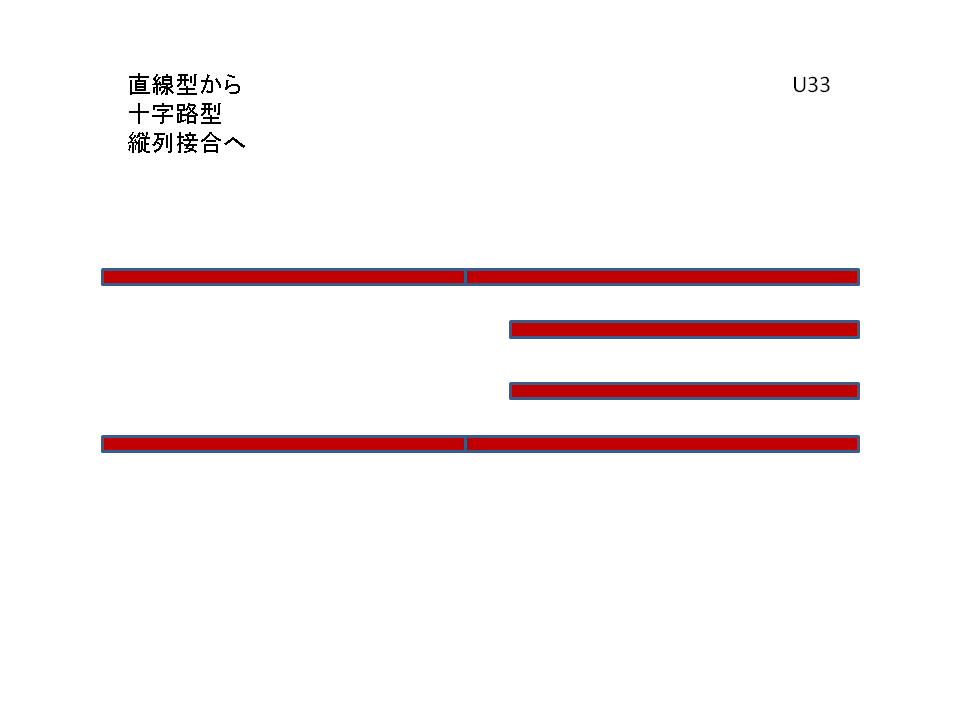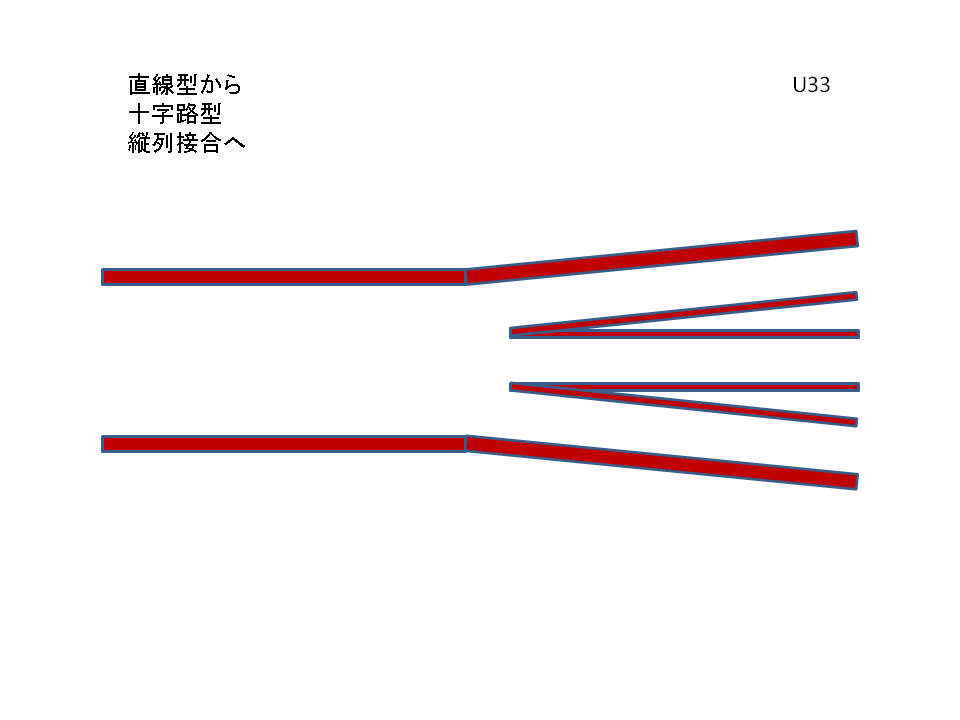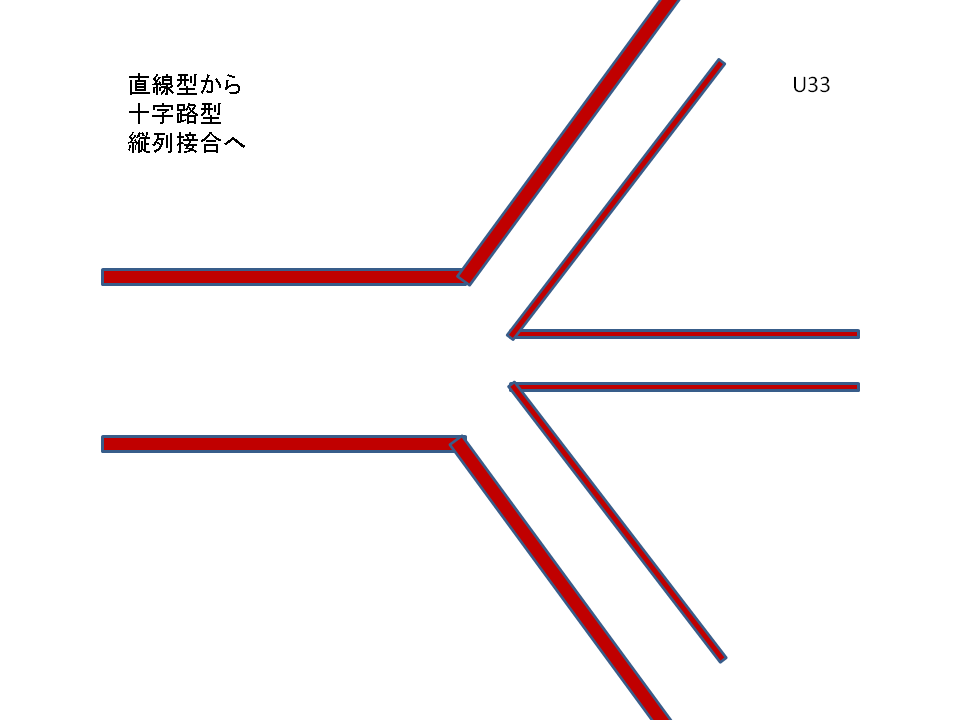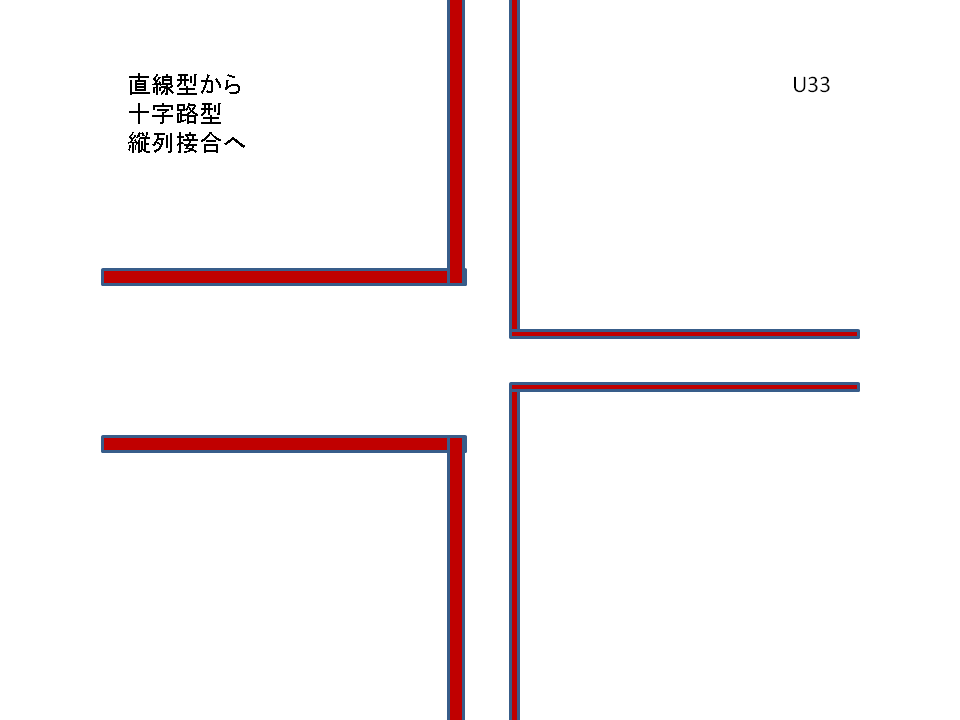
それには、B伝送路を構成するA&Bの銅板を「図:3」のように末端から裂き、基本伝送路の上下の銅板を又、上下に90度折り曲げますと、次の「図:4」のような伝送路系が形成されます。
この過程もアニメーションを御参考下さい。
 |
 |
 |
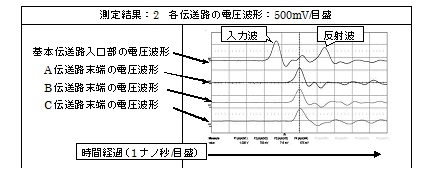
今回も「図:1」の場合とほぼ同一の電圧波形変化が観測されています。
(但し、基本伝送路での観測は、その入口部で行いましたので、他の伝送路の末端より早い時間に観測され、且つ、各伝送路末端からの反射波の合成波も観測されています)
 |
このような結果は、銅板に手形成される伝送路のみならず通常の伝送路(今回は同軸ケーブルを使用しました)に於いても観測されます。
即ち、長さ200メートルの同軸ケーブルを縦列結合した際の、各同軸ケーブルの末端での電圧観測結果を観測したのです。
(注:同軸ケーブルとは、テレビのアンテナからの引込み線のように、外側の線が金属の網線となっている円筒状のケーブルです)
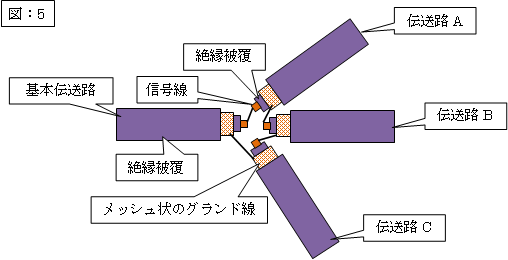
「図:5」のように結線し、電源(パルスジェネレータ)からのクロック信号(100KHz、出力電圧:1V)を1パルス基本伝送路に送り込み、各々200メートルの長さの同軸ケーブル3本の出力を電圧測定器(オシロスコープ)の3箇所の測定用の入力端子に送り込み、それらの電圧波形を測定しました。
 |
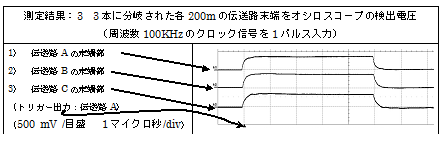 |
この測定結果を見ますと、予想通りに各伝送路から同型の出力波形が、同時刻に観測されています。
(測定結果下部の、黒の三角印がトリガー時刻であり、これと同時刻に各出力波が観測されています。
この同時刻に3本のケーブルの末端で電気信号の到着が観測された事実は、“電気がプラスからマイナスへと順次流れて行く”と言った小学校などで教わって来た電流の流れが正しいとしたら、1本の200メートルのケーブルで電気信号が観測されたら、次のケーブルで電気信号が観測される為には、このケーブルのもう一方の電線をお隣の電線との結線地点まで戻り、そのお隣の電線を伝って測定機まで電流が進まなくてはなりません。
即ち、3本のケーブルの末端での観測時間はそれぞれ、200メートル長のケーブルを往復する時間、約200ナノ秒(=200×100×2/20cm/ナノ秒)ずつずれている筈です。
しかし、今回の観測は、3本のケーブルの末端での観測時間は同時刻です。
ですから、この点からも、小学校以来教わって来た電流の流れに関する概念を払拭しなくてはなりません。
(参考の為に、独立したトリガー出力をオシロスコープに入力しつつ、各伝送路を個別に差動プローブを用いて観測しましたが、結果は同じでした。
勿論、4本の同軸ケーブルを同様に接続して測定しましたが、この場合も結果は同じでした。
これらの件は、自著『コロンブスの電磁気学』増補改訂版をご参照ください)
このような「縦列接合の存在」をお認め頂けましたら、先の拙文≪敬愛するマイケル・ファラデー(3)≫、≪敬愛するマイケル・ファラデー(4)≫で記述しましたファラデーが予測してもその結果が得られなかった現象。
そして、今回、ファラデーの予測通りの結果が得られた現象。
即ち、入力伝送路(能動伝送路)に入力した電気信号と同型の電気信号が隣接する伝送路(受動伝送路)にも観測される現象の仕組みを容易に理解出来ます。
それには次の概念図(「図:6-1〜3」)をご覧頂きますと直ぐにご納得いただけると存じます。
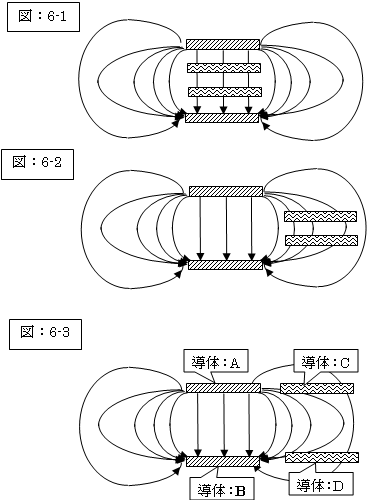 |
この概念図から、更に分かります事は、
| 私達は、「図:6-3」の如くに、導体A&Bが形成する能動伝送路として電気信号を流したつもりでも、 隣接する導体C&Dが形成する伝送路を入力伝送路(能動伝送路)とは、別の伝送路として受動伝送路と命名するのは私達の勝手で、 電気信号は、入力伝送路(能動伝送路)に、互いに縦列接合された「導体Aと導体Cの伝送路」、「導体Cと導体Dの伝送路」そして「導体Dと導体Bの伝送路」の3組の伝送路が 「図:6-1」と同様に縦列接合された伝送路(4本の導体で形成された伝送路)を流れる事になるのでしょう。 |
(斜めの導体間で伝送路を組むことも考えられましょう)
そして、その3組の伝送路の流れの中での、1組の伝送路(導体Cと導体Dの伝送路)即ち、受動伝送路を流れ得る電流分の存在をファラデーが予測して、今回実際に観測しただけなのです。
そして、その私達は、その1組の伝送路に流れる電気信号をクロストークと呼んでいるだけなのです。
(従って、クロストーク波形も本質的には入力波形と同型になるのです)
改めて、「図:6」を見ますと御気付き頂けると存じますが、
|
私達は、一般的には「終端処理」として、能動伝送路(導体A、導体Bよりなる伝送路)と、受動伝送路(導体C、導体Dよりなる伝送路)に、それら伝送路の特性インピーダンスに合致した値の抵抗(終端抵抗)をセットします。 (この終端処理によって、各伝送路を流れて来た電気信号は、全て各終端抵抗で過不足なく消費され、各伝送路での反射現象が皆無となります) ところが、導体A、導体Cよりなる伝送路、又、導体B、導体Dよりなる伝送路には全く抵抗がセットされておらず、即ち終端処理が施されておりません。 ですから、これらの伝送路では反射現象が発生します。 |
その現象とは、『能動受動2組の伝送路のそれぞれの末端を今回は抵抗で結合しましたが、抵抗を用いずにそのまま短絡(ショート)状態としても、何も接続せず開放(オープン)状態としても、受動伝送路にはマイナスの反射波が帰ってくるのです。』
この件に関しての更なる実験、考察は、自著『コロンブスの電磁気学』増補改訂版の「第12章 第2項 「差動伝送路系」で「クロストーク」の本質を」を御参考にして頂けたら幸いです。
| (「縦列接合」を御納得頂く為の補足実験) |
次なる実験は、どなたも御自宅で簡単に実験可能です。
是非お試し下さい。
(但し、電気を取り扱いますので、十分ご注意して下さい、そして、それに伴う事故に対しては当方は一切責任を負えません)
「図:4」或いは「図:5」と同種の伝送路系を、被覆線が赤と黒に分かれている1メートル長のスピーカーコード(或いは電源線)を2本用いて、次のように作成します。
(勿論、赤と黒に分かれていなくても良いのですが、説明しやすいので、赤/黒線を用いました)
各々のコードを50cm切り裂き「写真:1」のように赤線、黒線に分離します。
次に、「写真:2」のように、その切り裂き分離した赤線を、同じく切り裂き分離した黒線にスコッチテープで貼り合わせて新たな伝送路として、A伝送路、C伝送路を構成しました。
 |
そして、「写真:3」のように、基本伝送路のコードにはプラグを、他の伝送路コードにはコンセントをセットしました。
そして、この基本伝送路のプラグを家庭内のコンセント(テーブルタップ)に挿入して、各末端の電圧を、「写真:4」のように、順次1個のテスターで測定します。
 |
 |
このように、直接基本伝送路に機械的に接続されていないA、B、C伝送路の末端に電圧(約9ボルト)が観測されています。
(しかし、合算電圧は100ボルトに達していません。
この件は、次の拙文≪敬愛するマイケル・ファラデー(6) 縦列接合がコンデンサの謎を解く≫をご参照ください)
更に、3個のテスターを、各コンセントに同時にセットして観測しますと、各々のテスターは約33ボルトの電圧を表示してくれます。
(尚、2個のテスターを同時にセットして測定しますと、その測定値は各々約20ボルトを示しました。
更には、これらのケーブルをテーブルタップから外し、その代わりにテスターの先端をそのコンセントに挿入し、テーブルタップのスイッチをオンオフしてみますと、オンの場合は当然100ボルト程度を示しますが、オフの場合でも3ボルト程度を表示します。
この現象も、今回の実験と同様な現象によります)
このような測定方法(3個のテスター同時セット法)では、通常の電池でも観測可能です。
1.5ボルトの電池をプラグ部に接続すれば、各端子は、約0.5ボルトを示しますし、9ボルトの電池を接続すれば、約3ボルトを示してくれます。
(1個のテスターをセットして測定した場合は殆ど観測できません)
このように、テスト方法で検出電圧が変化するのは、テスターを接続した末端は接続しなかった末端との間に相違が生じる為です。
これらの件も含めて、次の≪敬愛するマイケル・ファラデー(6) 縦列接合がコンデンサの謎を解く≫をご参照ください。
否!その前に、次の補足もご参照ください。
(補足:縦列接合された伝送路に流れる電流値は同一である)
「コンデンサに関する新しい理論」を次で説明するのですが、その前に“縦列接合された伝送路に流れる電流値は同一である”点を認識しておいて頂きたいと存じます。
(尚、詳細は、自著『コロンブスの電磁気学』増補改訂版の「第6章第1項:伝送路を流れる電流」等をご参照ください)
前掲の「図:2」“導体堤防と電気的な相互作用を喚起しながら流れる電磁波川” のイメージ図を補いますと、このイメージ図で導体堤防と直接的な相互作用を誘起しているのは、そのイメージ図の一番上の「赤い波」、一番下の「青い波」のように見えますが、赤波の下、或いは青波の上の各波も同様な相互作用能力を有していて、各波間でその力をバランスさせながら流れていると推測できます。
(即ち、赤青の力を有しペアを組む波が各段、何組あろうと、隣接する赤の力、青の力が相殺され、次のイメージ図のように、結果的には赤青の力を有しペアを組む1組の波と等価となるでしょう。
この件は、先の等間隔に銅板が挿入された事によって形成された縦列接合された各伝送路の電圧の測定値が等しかったことからも立証されます)
従って、次の図のように「縦列接合された伝送路に同一の電流流れる」をイメージする事が可能となります。
では、次の≪敬愛するマイケル・ファラデー(6) 縦列接合がコンデンサの謎を解く≫をご参照ください。
|
|
『コロンブスの電磁気学』増補改訂版(A4判 831頁 価格:6000円) |
