『コロンブスの電磁気学』の要旨（12）　定常状態とは（2）

（敬愛するマイケル・ファラデー（12））

2011年3月14日

宇佐美　保

 

　前文≪『コロンブスの電磁気学』の要旨（11）　定常状態とは（1）≫並びに、ここまでの、コンデンサ、並びに、コイルに関する考察から、私達は電気の世界に於いて「定常状態」或いは「飽和状態」といった類の言葉を誤って用いていた事にお気付き頂いたと存じます。

 

　それでも、前文に於いては、コイル伝送路（高特性インピーダンス伝送路）を入出力伝送路に直列接合した場合で考察しましたが、本文に於いては、コンデンサ（低特性インピーダンス伝送路）を入出力伝送路へ、一般的な接続即ち縦列接合した場合で、「定常状態」を考察いたします。

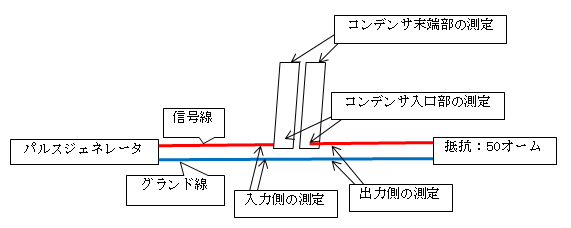
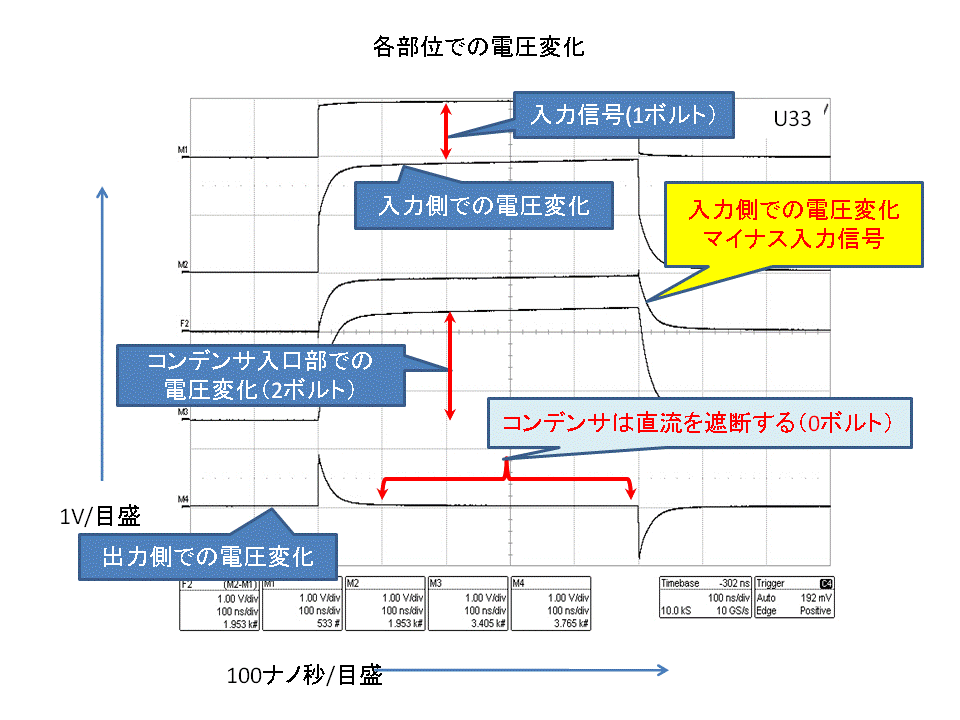
　そこで、先の≪敬愛するマイケル・ファラデー（7）　縦列接合がコンデンサの謎を解く≫に於いては「図：1」のように、パルスジェネレータ（1ボルト、1MHzの1パルスのクロック信号を出力）、銅箔コンデンサ（幅：5、長さ：10cm、Z_c:4.8Ω）、抵抗を同軸ケーブルで結び、コンデンサ入口部、入力側の伝路並びに出力側の伝送路に於ける電圧変化を測定しますと、次の「測定結果：1」を得る事が出来ました。

 

「図：1」（先文の「図：2」）

「測定結果：1」（先文の「測定結果：3」）

 

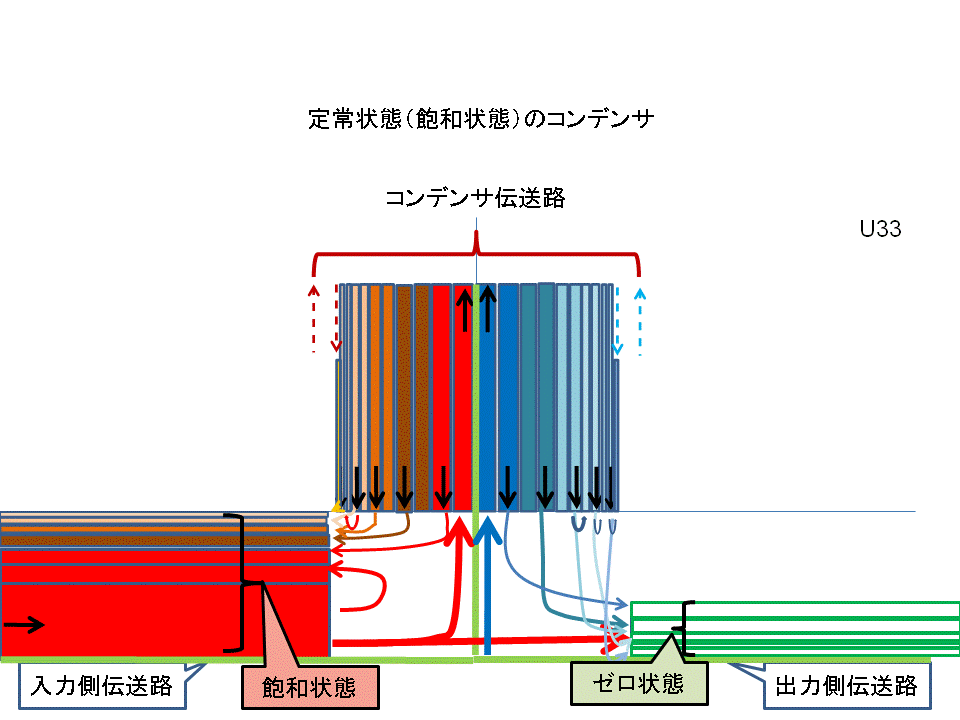
　　この測定結果での、「定常状態（飽和状態）」での、入出力伝送路並びコンデンサ伝送路内での電気信号の進行状態の「イメージ図：1」を、先文同様に表示しました。

 

　この件は、先の≪敬愛するマイケル・ファラデー（7）　縦列接合がコンデンサの謎を解く≫で十分御納得と存じますが、その図に於いては、プラス/マイナス電流を相殺して表示していますので、「イメージ図：2」に、プラス/マイナス電流を相殺せず各々の電流を個別に暖色系/寒色系と色分けして表示します

イメージ図：1	イメージ図：2

 

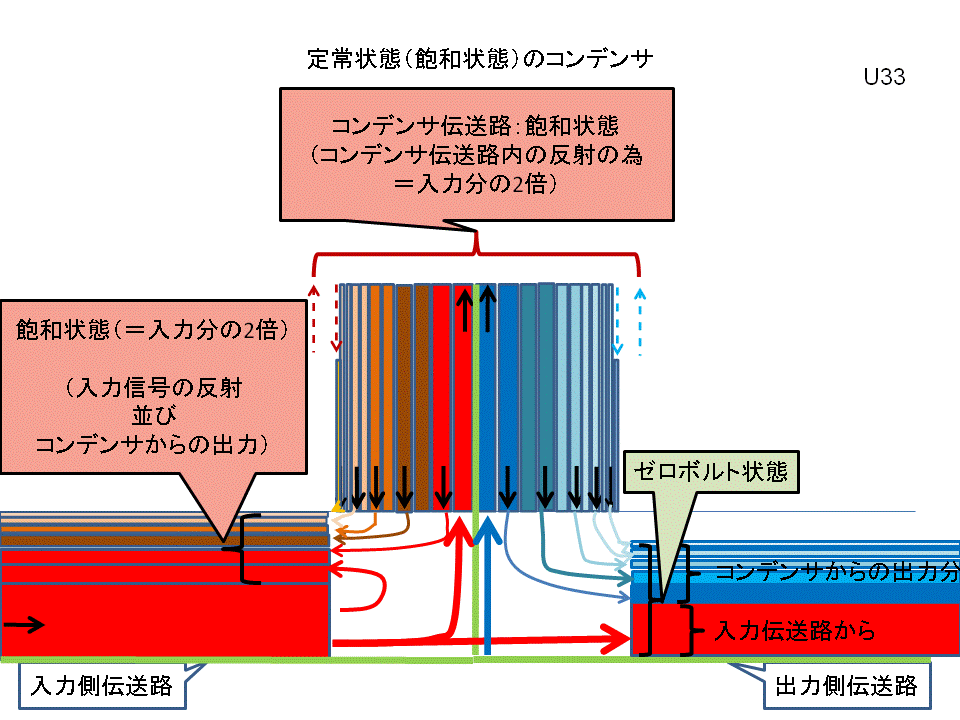　この「イメージ図：2」から、従来は“コンデンサは直流の流れを遮断する”と言われてはいましたが、コンデンサが直流の流れを遮断するのではなく、入力伝送路から出力伝送路へ直接的に流れる電流（プラス）を、コンデンサは、コンデンサから流出するマイナス電流で相殺しているだけである事が分かります。

 

　この件は「イメージ図：1＆2」だけではなく、前文同様に、これらイメージ図の作成根拠としての表計算ソフト（Excel）での計算の推移を掲げさせて頂きます。

 

尚、計算の根源として、入力伝送路から縦列接合されているコンデンサ並び出力伝送路への反射係数（τ）は、

τ＝（（4.8+50）−50）/（（4.8+50）+50）＝0.0458

1−τ＝0.9542

逆に、コンデンサ伝送路から、そこに縦列接合されている入力伝送路並び出力伝送路への反射係数（τ_c）は、

τ_c＝（（50+50）−4.8）/（（50+50）+4.8）＝0.9084

1−τ_c＝0.0916

 

但し、前文同様に、電流値に関しては、入力伝送路へ基本電流：1を流した場合で計算し、又、「測定結果：1」は、同軸ケーブル（Z=50Ω）へ、電源から入力伝送路へ1ボルトの電気信号した場合ですから、その際の電流値は0.02アンペア（＝1/50）であることは明らかです。

従って、最終的に各部での電圧値を比べるに当たっては、表計算ソフトで得られた電流に、0.02を乗じた値を、各伝送路を流れる電流値として計算し直す事が必要です。

（赤字はプラス、青字はマイナス）

 

表：1
	入力側伝送路			コンデンサ伝送路		出力側伝送路
反射回数	基本電流	コンデンサからの反射電流	コンデンサからの流出電流	入力側からの電流	コンデンサ末端からの反射電流	入力側からの電流	コンデンサからの流出電流
0	1.0000	0.0458		0.9542			0.9542
1			0.0874		0.8668	0.0874
2			0.0794		0.7874	0.0794

 

　しかし、この表の表示を簡略化し（計算を続行し）て、次の表を得ました。

 

表：2
往復回数	コンデンサから 入力伝送路へ	コンデンサ伝送路 末端から	コンデンサから 出力伝送路へ
1	0.087407	0.954198	0.087407
2	0.079401	0.866791	0.079401
3	0.072127	0.78739	0.072127
4	0.06552	0.715263	0.06552
5	0.059518	0.649743	0.059518
6	0.054066	0.590224	0.054066
7	0.049114	0.536158	0.049114
8	0.044615	0.487044	0.044615
9	0.040528	0.442429	0.040528
10	0.036815	0.401902	0.036815
11	0.033443	0.365086	0.033443
12	0.03038	0.331643	0.03038
13	0.027597	0.301264	0.027597
14	0.025069	0.273667	0.025069
15	0.022772	0.248598	0.022772
16	0.020686	0.225826	0.020686
17	0.018791	0.20514	0.018791
18	0.01707	0.186348	0.01707
19	0.015506	0.169278	0.015506
20	0.014086	0.153772	0.014086
……	……	……	……
150	5.3E-08	5.79E-07	5.3E-08
各電流の合計	0.9542	10.42	0.9542

 

　この結果から、先ず入力伝送路側への、コンデンサからの反射並び流出電流の合算値（コンデンサ伝送路内の往復回数が150回までの合算値ですが、ほぼ飽和値に達して居ります）は、

 

コンデンサからの反射並び流出電流の合算値

0.0458+0.9542＝1

コンデンサ内を往復する電流の合計は、この表からそのまま、10.42

この電流値を、（入力伝送路に1ボルト流した場合の）電圧に換算しますと、

10.42×0.02アンペア＝0.2084アンペア

従って、この電流によるコンデンサ伝送路（Z_c：4.8Ω）の電圧は

コンデンサ伝送路（Zc：4.8Ω）の電圧

0.2084×4.8＝１ボルト

　更に、これらのコンデンサ内電流は末端と入口間を往復していますから、コンデンサ内の電圧は、これらの２倍である2ボルトが、「測定結果：1」」が得られる事になります。

 

　一方、出力伝送路側への、入力伝送路からの直接流出電流と、コンデンサからの流出電流の合算値は、

出力伝送路側への、入力伝送路からの直接流出電流と、コンデンサからの流出電流の合算値

0.9542+（-0.9542）＝0

と、出力伝送路には、コンデンサを通して、直流電流が流れないと表現するのではなく、“入力伝送路からの出力されたプラス電流を、コンデンサからの流出電流が相殺する”と認識すべきなのです。

 

　以上の考察は、コンデンサ伝送路内電流の150回の反射現象に基づき考察していますが、この反射現象は、入力信号が続く限り（コンデンサ内に電流が残存している限り）繰り返されますし、その反射現象（入口部）の結果、絶えず、入出力側へと電流が排出されているのです。

（但し、反射のたびに、電流値は小さくなり、ゼロへと収束して行きますから、その往復電流の合算値もある一定値へと収束して行きます）

 

　以上の「イメージ図」、「計算」では、コンデンサ伝送路長（ある意味では、コンデンサ容量）、又、入力信号（クロック信号）の周波数には、無関係で行ってきました。

従って、逆に、ここまでの考察は、これらの因子には無関係なコンデンサに関しての根本的な考察である事がお分かり頂けると存じます。

この件を明確にする為に、先の「図：1」同様に接続した、銅箔コンデンサ（幅：5、長さ：10cm、Z_c:4.8Ω）に、電源（パルスジェネレータ）から、1MHz（高周波信号）、並びに1KHz（低周波信号）の1パルスのクロック信号（1ボルト）を出力して、それぞれの場合の出力伝送路への出力波形を測定し、次の「測定結果：2」を得ました。

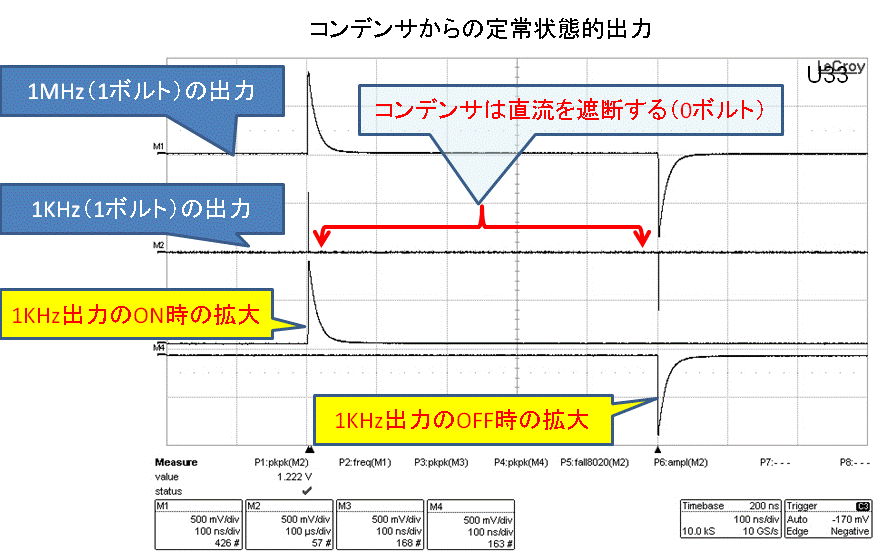
この結果の出力波形の全体像（上部２つの両者の測定結果）を比較しますと、従来言われてきたように、高周波信号（1MHz）では、その信号のオンオフ時の出力波形が認められるのに反して、低周波信号（1KHz）の場合には、“コンデンサは直流を通さない”の従来説の通りの結果が得られているように見えます。

 

　と申しましても、低周波信号（1KHz）の場合でも、その信号のオンオフ時に棘状の電圧突起が認められます。

そこで、この２つの棘状の突起部分（100マイクロ秒/目盛で表示）を、1MHzの場合同様な時間軸（100ナノ秒/目盛）に拡大して観測して、下部の２本の測定結果を同一画面（1MHzの凹凸波形の位置に合わせて（オフ時の波形を時間的に移動））に掲げました。

測定結果：2	測定結果：3　 （「測定結果：2」に基づき 高周波の出力と低周波の出力の比較）

 

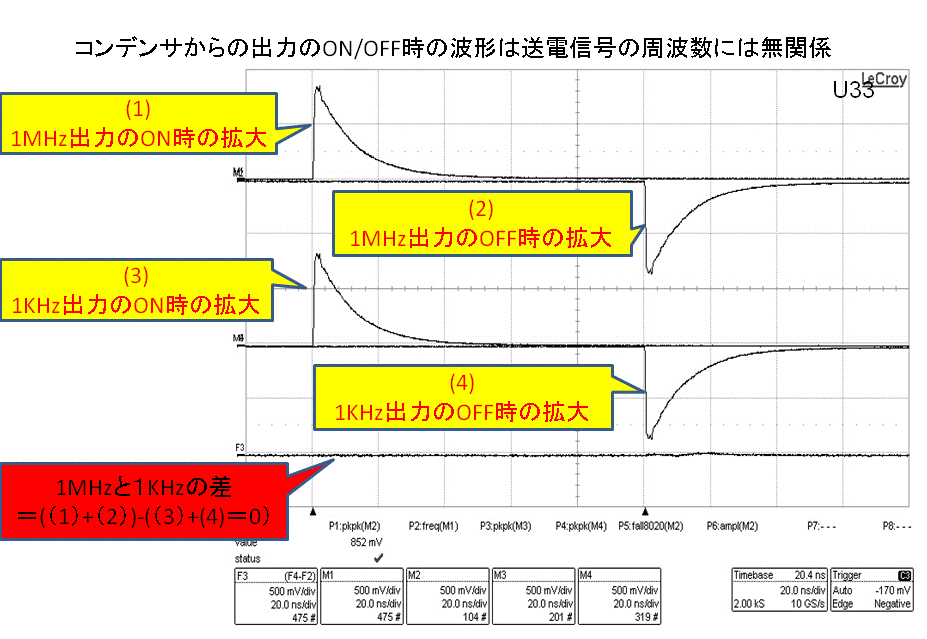　この「1KHzの関する下部の２本の測定結果」は、1MHzの測定結果と同形であると見られます。

　そこで、1ＫＨｚ並び1ＭＨｚの立ち上がり部立下り部の波形を20ナノ秒/目盛に拡大して両者の差をオシロスコープ内で計算しますと「測定結果：3」に見ますように、両者の差はゼロであって、高周波信号（1MHz）でも低周波信号（1KHz）の場合、その信号のオンオフ時の一定期間中に於いては同一形状の出力波形が認められる事が分かります。

 

　この点を換言すれば、コンデンサを流れる電流は高周波であっても低周波であっても（直流であっても）今回の考察（イメージ図）の通りに、その流れ方は同一であることが分かります。

（良く見ますと、両者ともその波形は同じ段階的に変化している事が分かります）

 

 

（補足）

　従来の“コンデンサを流れる電流は変位電流” 並び“コンデンサは電荷を蓄える”の破綻

 

（1）  「変位電流説」の破綻

　前述の繰り返しになりますが、今回の考察（計算結果に基づくイメージ図と測定結果の一致性）から、“電流は流れていないのではなく、入力伝送路からの直接的な電流は流れ続けており、一方、コンデンサからも出力伝送路へ電流は流れ続けているのです。

但し、コンデンサ内電圧が飽和状態となると、流出電流値は、入力伝送路からの電流値と同じ値となり、これらの流出される電流の正負符号が逆である為、それらが互いに相殺し合い、見かけの電流値がゼロとなるのです。

 

従いまして、“コンデンサ内の電荷量が飽和状態では電流は流れない”との“変位電流説”は破棄されるべきなのです。

 

（2）  「コンデンサは電荷を蓄える」並び「電流は電荷の移動」説の破綻

 

　従来の電流並びコンデンサ論では、コンデンサに流れ込む一定電流（I）と、コンデンサに蓄えられる電荷量（Q）は、は、次の関係がある

I=dQ/dt

と説明されて来ました。

又、その際の、コンデンサの両電極間の電圧（V）とコンデンサ容量（C）の、

Q=CV

との関係から、

I=CdV/dt

の式が示されていますが、このような関係式からでは、コンデンサ内の電圧変化の段階的変化などを説明する事は全く出来ません。

 

（3）  更に付け加えますと

 

先も今回での測定考察結果から、コンデンサ伝送路内電圧は入力信号電圧の２倍と計測も計算もされます。

ところが、上記しましたように、容量がCのコンデンサに蓄えられる電荷量（Q）は、そのコンデンサに印加される電圧（V）に比例する、

即ち　Q=CV

と教えられてきた私達は、コンデンサの飽和時の電圧が2Vとなる事を知った今では、従来のコンデンサに関する理論は破棄しなくてはならないのです。

　では次の≪『コロンブスの電磁気学』の要旨（13）　単独と連続パルス（1）≫に移らせて頂きます。