（敬愛するマイケル・ファラデー（11））

2011年3月7日

宇佐美　保

 

　ここまでの、コンデンサ、並びに、コイルに関する考察から、私達は電気の世界に於いて「定常状態」或いは「飽和状態」といった類の言葉を誤って用いていた事にお気付き頂いたと存じます。

 

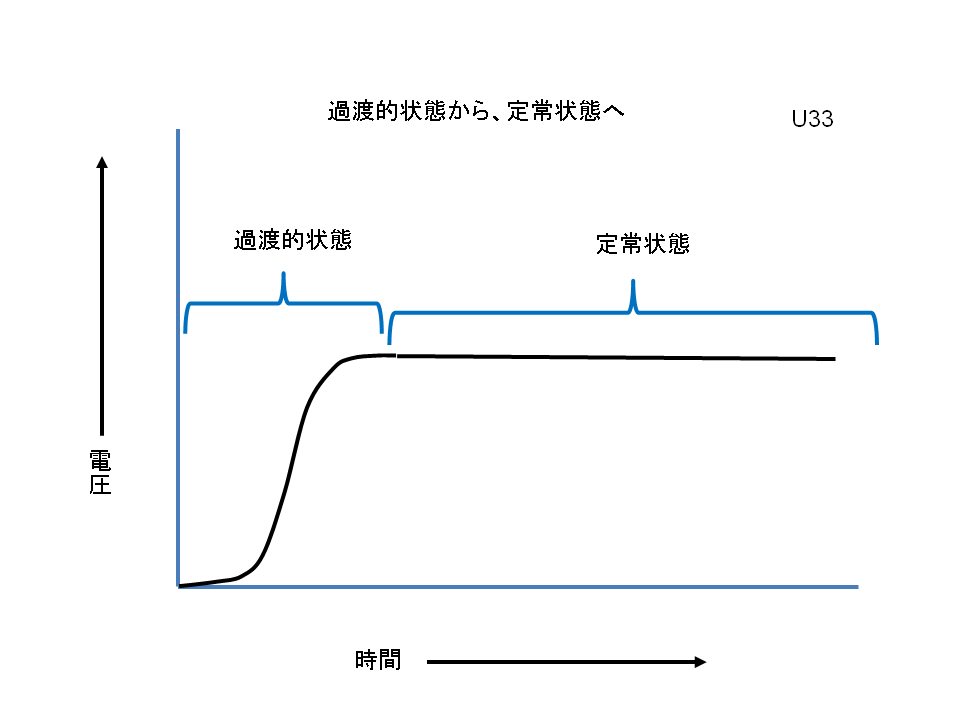
　例えば、直流（クロック信号）を電気回路に流し、ある個所で電圧を測定すると多くの場合は次の「イメージ図：1」のような、時間と電圧の関係を得る事になります。

 

　そして、電圧がゼロから立ち上がって一定値に落ち着くまでの期間を「過渡的状態」と表現したり、又、一定値に落ち着くと「定常状態」に到達した（或いは「飽和状態」に達した」……）と表現したりしてきました。

イメージ図：1	イメージ図：2

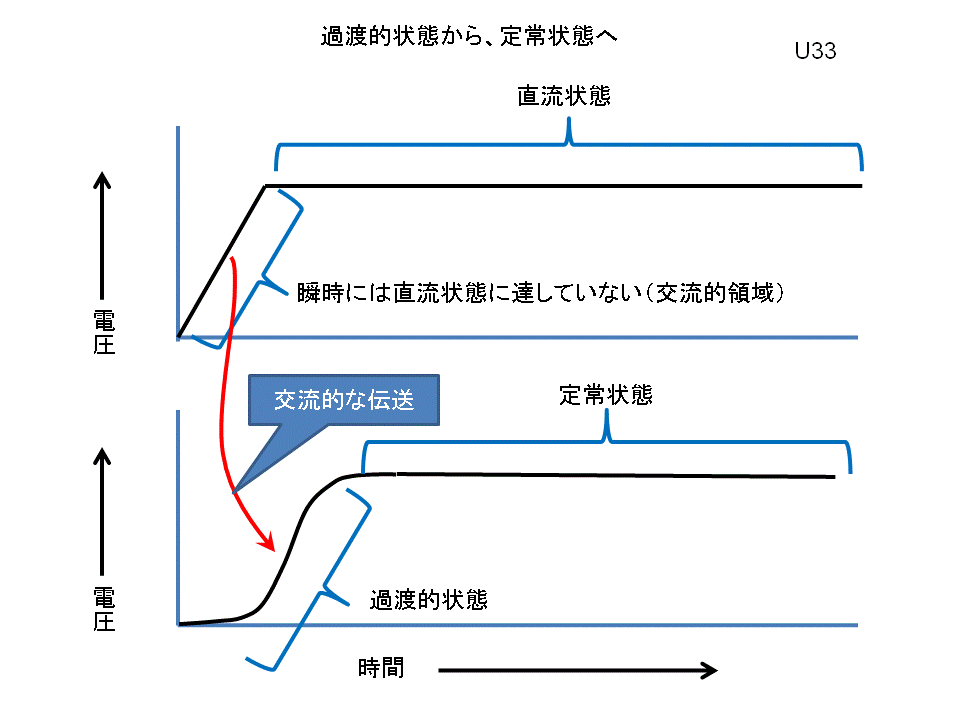　そしてこのような状況になる原因として、「イメージ図：2」のように、直流（クロック信号）流したと言っても、その信号自体が、瞬時には所期の電圧に達していないので、この部分の伝送に関しては「直流伝送」ではなく「交流的伝送」になり、その結果「過渡的状態」が出現し、その後は「直流伝送」となるので、当然「定常状態」の伝送模様を観測する事になる。

即ち、“「定常状態」での伝送こそが、「直流そのもの」の伝送である”と聞かされたりしませんでしたか？

しかし、≪『コロンブスの電磁気学』の概略≫の「3　直流も交流も同じ電気」）にも書きましたが、その題目通りに、“直流も交流も同じ電気”ですから、伝送状況も同じであるべきなのです。

 

　そこで、直近の例として、前文≪コロンブスの電磁気学』の要旨（10）　直列接合のコイル≫に於ける、入出力伝送路を同軸ケーブル（Z=50Ω）、それらに直列し、挿入したコイル伝送路をフィーダー線（Z_c：300Ω）として、クロック信号を1パルス流した際の「出力側伝送路への出力信号」の「測定結果：1」と、それに対応する「イメージ図：6」の、「入力側への逆流信号」並び、「出力側伝送路への出力信号」をご覧頂ければ、従来説が誤解の産物であった事が明々白々となると存じます。

前文の「測定結果：1」	イメージ図：3　（前文の「イメージ図：6」）

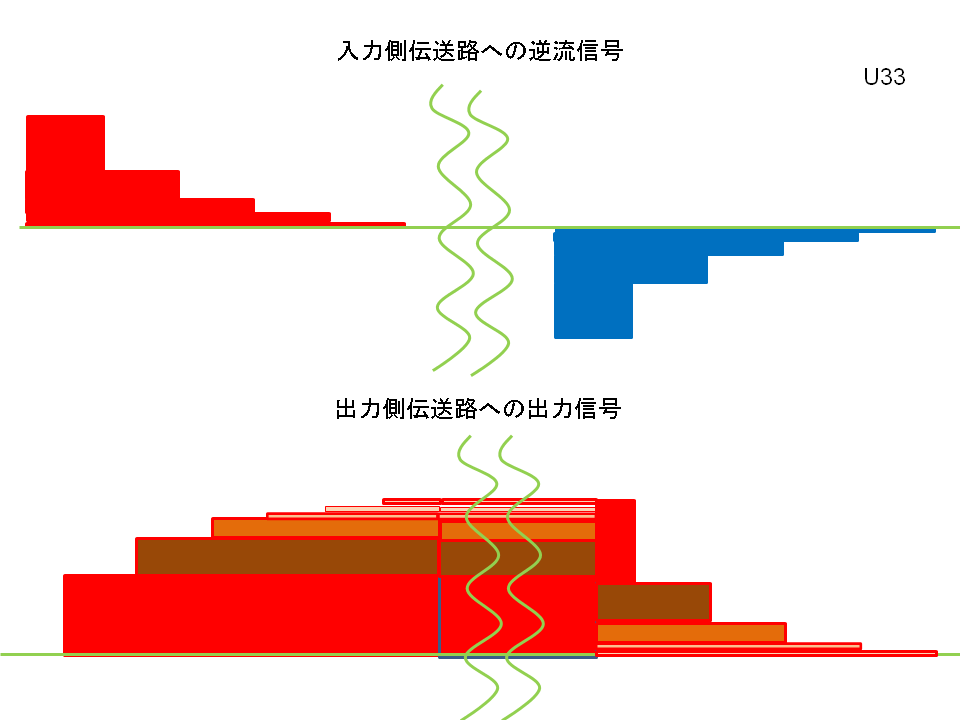　何しろ、この「イメージ図：3」を描くに当たっては、入力クロック信号の立ち上がりは瞬時としていますから、今まで言われている「交流成分の伝送」は皆無なのです。

 

　この「イメージ図：3」作成の根源として、入力伝送路からコイル伝送路への反射係数（τ）は、τ＝（300-50）/（300+50）＝0.714

逆に、コイル伝送路から、入力伝送路、出力伝送路への反射係数（τ_c）は、

τ_c＝（50-300）/（50+300）＝−0.714

を用いて、表計算ソフト（Excel）にて、次の手順で求めて行きます。

 

尚、電流値に関しては、入力伝送路へ基本電流：1を流した場合で計算しました。

この基本電流：1を1アンペアとして計算せずとも、「測定結果：1」は、同軸ケーブル（Z=50Ω）へ、1ボルト出力した場合ですから、その際の電流値：0.02アンペア（＝1/50）として、表の各値に、0.02を乗じた値を、各伝送路を流れる電流値として計算し直すも妥当である事は言うまでもありません。

 

表：1
入力伝送路			コイル伝送路		出力伝送路
基本電流	コイル伝送路からの 反射電流	コイル伝送路側からの流出電流	出力側へ向かう電流	入力側への逆流電流	コイル伝送路からの電流
1	0.714		0.286	→	0.4902
		0.35	←	0.2042
			0.146	→	0.25
		0.178	←	0.104
			0.074	→	0.127
		0.91	←	0.053
			0.038	→	0.065
		0.0464	←	0.027
			0.0193	→	0.0331
		0.0236	←	0.0138

 

　しかし、この表のように電流方向を示す矢印が存在すると、各電流の合計が簡単にも止まらないので、矢印を省略して、次の表を得ました。

（赤字はプラス、青字はマイナス）

 

 

（コイル内電流の合算値：0.166＝0.583+（−0.417））

 

　この計算結果を基として、先ず、入出力伝送路コイル伝送路間の反射現象の結果として、入力側への電流について考察しますと、プラス電流は「表：1」から、0.714であり、マイナス電流は、この「表：2」から0.714と同じ値が読み取れますから、入力伝送路を流れる電流は、基本電流の“1”のみとなります。

 

　そして、この値が、コイル伝送路から流出する「出力伝送路」への電流（＝1）と等しくなっております。

 

　そして、「コイル伝送路」に存在する電流分は、「表：2」から、0.583−0.417＝0.166　となります。

そこで、入出力伝送路（Z=50Ω）と、このコイル伝送路(Z_c＝300Ω)との電圧比較には、この0.166の値に300/50を乗じて、“1”（入出力伝送路での値に同じ）を得ます。

 

但し、この操作よりも、実電流での計算の方が分かり易いと存じますので、先に求めた0.02アンペアを基本電流としますと、入出力側の電圧は当然、1ボルトになり、コイル伝送路でも、この値同様な　0.02×0.166×300＝1ボルトを得ます。

　

　従って、「過渡的特性」として、「イメージ図：2」のように解釈するのは不当である事が分かります。

更に、注意すべき点は、「定常状態」と言われている状態でも、入力伝送路側から「直流的信号」がコイル伝送路を通して、そのまま出力伝送路へ流れているのではない事です

 

　入力伝送路には常に、コイル伝送路の接合点からの「プラスの反射電流」とともに、コイル伝送路からのマイナスの逆流電流が相殺している点です。

そして、コイル伝送路内も、常に入出力側の両端でマイナス反射を繰り返し、プラスとマイナスの電流の差分（プラス電流）が出力伝送路へ排出されているのです。

 

　この件を、前文の「イメージ図：5」を再掲し、並び、その補足説明を加え次に示します。

前文の「イメージ図：5」	前文の「イメージ図：5」の補足説明

そして、更に、このイメージ図で、プラス/マイナス電流が相殺された部分を、改めて、プラス/マイナス電流に分離して書き加えますと、次の「イメージ図：4」を得る事になります。

イメージ図：4

 

　このイメージ図を見れば、外見的には「一定電流の定常的」に、入力伝送路側から、コイル伝送路を経由して出力伝送路への流れる状態、即ち、いわゆる「定常状態」といえども、内情は、各伝送路の特性インピーダンスの不連続点での反射現象が常に生じており、その結果各種の値の電流がそれらの伝送路を行き来しているのです。

（この反射は、「表：2」では、その回数が100回までの結果を表記していますが、コイル伝送路内に電流が存在する間は、際限なく繰り返されることは明らかです）

 

 

　このような状況は、何も今回のように入出力伝送路の特性インピーダンスよりも大きな特性インピーダンスを有する伝送路（コイル伝送路）を直列接合した場合に限定して発生するのではなく、逆に挿入される伝送路の特性インピーダンスが小さいコンデンサ的伝送路を直列接合した場合（先の≪『コロンブスの電磁気学』の要旨（8）≫の「図：3」）にも発生します。

即ち、電源（パルスジェネレータ）から、1MHz（1ボルト）のクロック信号を1パルス、出力して、次の測定（先の文の「測定結果：2」）を得ました。

更には、この測定結果に対するイメージ図（先の文の「イメージ図：6」（上）とその補足（下））を掲げます。

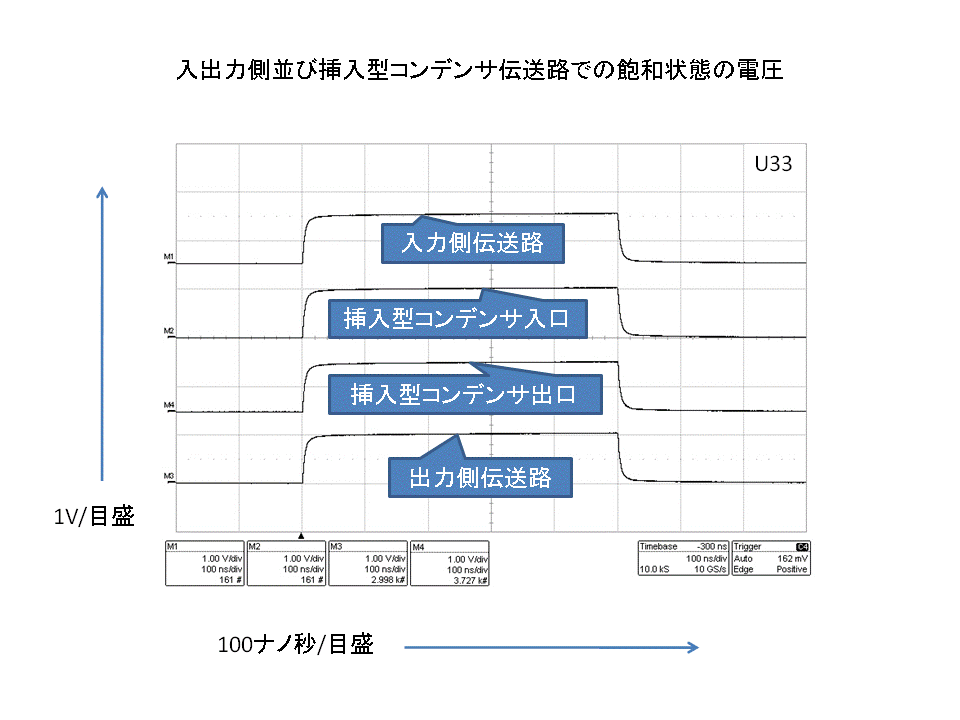
先の文の「測定結果：2」	「イメージ図：5」 先の文の「イメージ図：6」とその補足

 

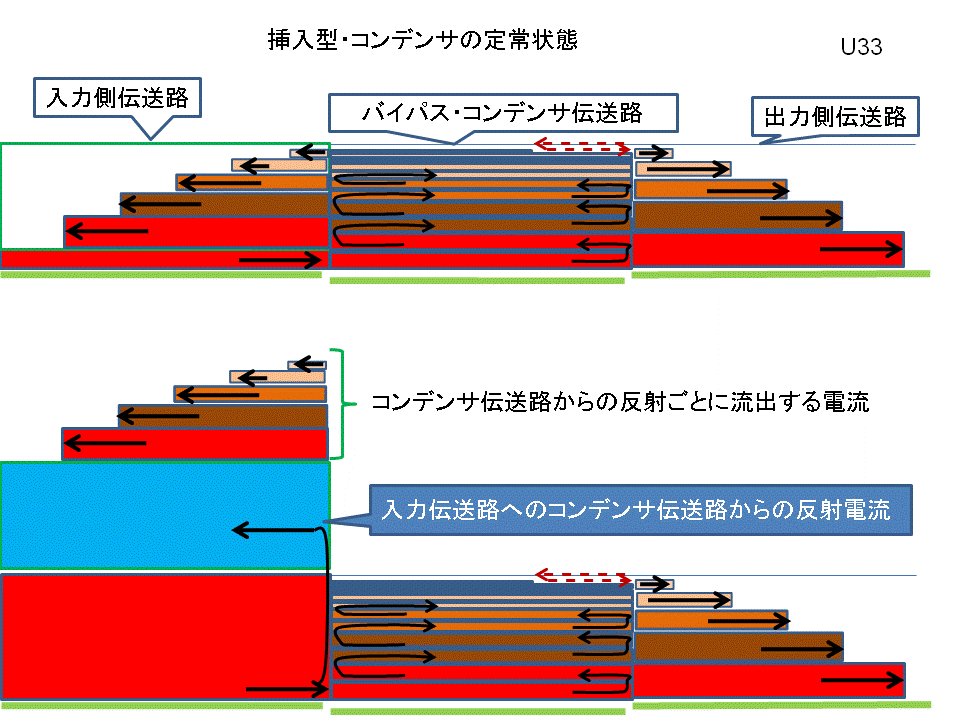　このように、「測定結果」では、「イメージ図：1＆2」の状況に見えますが、事実は「イメージ図：5」のように、上掲の高特性インピーダンス伝送路を直列接合した場合同様に、今回の場合のように低特性インピーダンスを直列接合した場合に於いても、各伝送路の特性インピーダンスの不連続点での反射現象が常に生じており、その結果各種の値の電流がそれらの伝送路を行き来しており、入力側では、プラス/マイナス電流の相殺作用が認められ、コンデンサ伝送路内では反射電流（プラス）の合算値の絶え間ない増大、そして、出力側ではそれに応じる出力値の増大が認められるのです。

（しかい、反射を繰り返すごとに反射電流自体が減少するので、ある一定の飽和値に収束しています）

 

 

　この「イメージ図：5」作成の根源として、上掲のコイル伝送路の場合同様に、表計算ソフト（Excel）にて、次の手順で求めて行きます。

 

入力伝送路からコンデンサ伝送路（Z_c＝4.8Ω）への反射係数（τ）は、τ＝（4.8−50）/（4.8+50）＝−0.825　逆に、コイル伝送路から、入力伝送路、出力伝送路への反射係数（τ_c）は、

τ_c＝（50-4.8）/（50+4.8）＝0.825

を用いて、入力伝送路へ基本電流：1を流した場合で計算しました。

 

表：3
入力伝送路側			コンデンサ伝送路		出力伝送路側
基本電流	コンデンサ伝送路との反射電流	コンデンサ伝送路からの電流	出力側へ向かう反射電流	入力側へ向かう反射電流	コンデンサ伝送路からの電流	入力伝送路からの電流
1	-0.8248		1.8248	→	0.3197	1.8248
		0.2637	←	1.5051
			1.2415	→	0.2175
		0.1794	←	1.0240

 

　更に、先のコイル伝送路の場合同様にして次の「表：4」が得られます。
（赤字はプラス）

 

表：4
	入力伝送路	コンデンサ伝送路		出力伝送路
反射回数	コンデンサ伝送路からの電流	出力側へ向かう反射電流	入力側へ向かう反射電流	コンデンサ伝送路からの電流
1	0.2637	1.8248	1.5051	0.3197
2	0.1794	1.2415	1.0240	0.2175
3	0.1220	0.8446	0.6966	0.1480
4	0.0830	0.5746	0.4739	0.1007
5	0.0565	0.3909	0.3224	0.0685
6	0.0384	0.2659	0.2194	0.0466
7	0.0261	0.1809	0.1492	0.0317
8	0.0178	0.1231	0.1015	0.0216
9	0.0121	0.0837	0.0691	0.0147
10	0.0082	0.0570	0.0470	0.0100
11	0.0056	0.0388	0.0320	0.0068
12	0.0038	0.0264	0.0217	0.0046
13	0.0026	0.0179	0.0148	0.0031
14	0.0018	0.0122	0.0101	0.0021
15	0.0012	0.0083	0.0068	0.0015
	……	……	……	……
100	7.24E-18	5.01E-17	4.13E-17	8.78E-18
電流の合算値	0.8248	5.7083	4.7083	1

（この表では、反射回数を100回にとどめて居りますが、現実は、対象となるコンデンサ伝送路内に電流が存在する限り、当然ながら、電流の反射は繰り返されます）

 

　この「表：3＆4」から、入力伝送路では、コイル伝送路との反射電流（-0.8248）と、コンデンサ伝送路から流出する電量の合算値（0.8248）が相殺され、入力伝送路を流れる電流値は、入力電流値に収束します。

しかし、この計算の相殺作用は反射現象が続く限り繰り返されます。

そして、出力伝送路の合算電流値は“1”となりますから、入力電流“1”がそのまま、出力された様相になりますが、実態は、「イメージ図：5」通りに、コンデンサ伝送路に電流が存在する限りコンデンサ伝送路との反射現象が繰り返して発生している結果なのです。

 

　一方、コンデンサ伝送路内の電流は、「出力側へ向かう反射電流の合算値：5.7083」と「入力側へ向かう反射電流の合算値：4.7083」の和：10.4166となります。

先の場合同様に、基本伝送路（Z=50Ω）に1ボルトの電圧を印加している場合には、この電流が、コンデンサ伝送路（Z_c＝4.8Ω）内に、電圧を発生させますが、その値Vは、

V=10.4166×（4.8/50）＝1ボルトと計算されます。

 

そして、この値も、コンデンサ伝送路に於いても、常に反射現象が発生している結果なのです。

 

　今回の実験並び考察からお分かり頂けますように、伝送路中に特性インピーダンスの不連続部分があれば、常に反射現象が発生して、従来「定常状態」と認識されていた状態は、その反射の合算結果が飽和状態と認識されるだけである事が分かります。

　くどいようですが、「飽和状態」であっても常に反射現象が発生している事は言うまでもありません。

 

 

 

 

（補足）又、くどいようですが「線間容量」について

 

 　先の≪『コロンブスの電磁気学』の要旨（8）　縦列接合以外のコンデンサ≫に於いて“「線間容量（並びにコンデンサの容量）」と言う言葉も「俗説」となって頂かなくてはならないのです”と記述しましたが、今回の記述からも更にこの点を御納得頂けたと存じます。

 

 　何しろ、従来説では、対象となる線（伝送路）を電気信号が流れる際には、当初その線間に、「相当量の電荷」を蓄えつつ流れなくてはならない為、送電すれるべき電気信号の一部を減少させつつ流れなくてはならない。

そして、十分に線間に電荷が蓄えられた後には、「定常状態」の送電となり、電気信号は、その量を減少することなく送電され、電気信号が流れ去った後（電気信号がオフとなった後）には、逆にこの線間に蓄えられていた「相当量の電荷」が放出され伝送される。

 

　この「相当量の電荷」が「線間容量」に相当し、この「相当量の電荷」の蓄積、放出現象の結果、冒頭に掲げました「イメージ図：1＆2」に見られる「信号オンオフ時の立ち上がり立下りとの鈍り（電圧の上昇下降の時間的な遅れ）」が発生し、この電荷の出し入れが不要となっている時間帯では電流は「定常状態」で流れると、私達は教えられて来たのです。

 

　しかし、今回の直列接合されたコンデンサ伝送路（Z_c：4.8Ω）の件はともかく、電荷の蓄積には無縁のコイル伝送路（フィーダー線　Z_c：300Ω）を直列接合した場合の結果からもお分かり頂けますように、「イメージ図：1＆2」に見られる「信号オンオフ時の立ち上がり立下りとの鈍り」が発生している点からも、「線間容量」は死語となって然るべきと存じます。

 

　それでも未だ「線間容量」の用語の使用を望まれるのなら、コンデンサとしての（いわゆる）容量値を定義するに当たっては、対称となるコンデンサ伝送路の特性インピーダンス値、並びに、それに接続される入出力伝送路の特性インピーダンス値によって変化する事を留意しなくてはならないのです。

（この点は、今回の反射状況を計算処理する際に、これらの数値を利用している事からもお分かり頂けると存じます）

 
　次は,この件を引き継ぎ≪『コロンブスの電磁気学』の要旨（12）　定常状態とは（2）≫に移らせて頂きます。