第17話

表皮効果という誤解された電気抵抗

 

2016年6月17日　宇佐美　保

 

　先の『第13話　トランスの理論も誤解です』に於いて、“「交流送電の伝送ロス」は、「電線の抵抗起因」だけではないのです”と記述しましたが、「表皮効果」という誤解された現象が存在します。

 

表皮効果  （skin effect）　　（世界大百科事典（日立デジタル平凡社）より抜粋） ……電磁場の振幅は，   だけ進むごとに1/e に減衰していく。すなわち電磁波は金属内に深く入りこむことができずにその表面近くに局在することになる。これを表皮効果といい，δ を表皮効果の厚さまたは表皮厚さという。電磁波が表面近くに局在するということは，導体の有効な大きさが減少することであり，そのぶんだけ電気抵抗が増える。電気材料としてよく用いられる銅では，周波数 ν の電磁波に対しては，δは，     から計算でき，たとえば ν＝3×1010Hz(波長1cm)のマイクロ波の場合 δ＝0.4μmとなり，ほとんど内部に進入できない。ν＝50Hzの交流では δ≒1cmであるから通常はほとんど問題にならないが，大電力を長距離送電する場合などには考慮されなければならない。

 

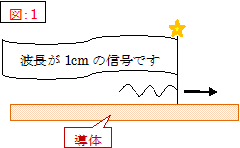
　本著に於いて、何度も記述していますが「電気は近接作用」（「電気も近接作用）ですから、電気信号が導体（電線）進行する際に、次の「図：1」のように、その電気信号の先に“これから波長が1cmの交流波が通ります”等と旗など立てて進まないのです。

又、その横に掲げた「図：2」をご覧いただければ、「従来の表皮効果説」に関しては、もうとやかく言うことなくご退場願うより他はありません。

 

 

 

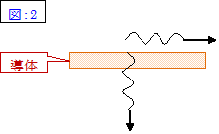「電気は近接作用」ですから、例えば、導体が（私達が）“今通り過ぎたのは、3×1010Hz(波長1cm)の電気信号”だと認識するには、少なくとも、「図：2」に示すように、電気信号（少なくとも1周期分）が通り過ぎた後に“ああ！今3×1010Hzの電気信号が”通って行ったと認識するのです。

 

 　その際には、導体内部には、既に、少なくとも1周期分(波長1cm)の電気信号が入り込んでいるのではないでしょうか？それなのに空気中を既に1cmも先に進行した後、或は導体中の空気中の1cmに相当する距離を入り込んでいるのに、“信号さ〜〜〜ん！あなたの導体内への侵入資格は、0.4μmですよ！”と後ろから叫ばれても、電気信号は困ってしまうでしょう。

50Hzの場合では、約6000k�b（＝約30万k�b/50）も先行しています。

その時までに、電磁波は導体内に冒頭に引用しました解説に於けるδ≒1cmに示される1cm以上を遥かに超える長い距離を侵入しているでしょう。

 

　このように、ファラデーが唱えた「電気は近接作用」を全く無視した「表皮効果説」が未だに信奉されているのが、私には不思議でなりません！

 

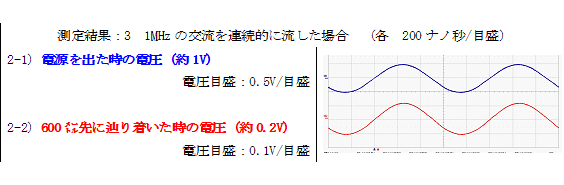
　この「表皮効果」が誤解されていることに関しては、以上の「思考実験」で十分でしょうが、これまで度々使用している「電源（パルスジェネレータ）」、「電圧測定器（オシロスコープ）」間を、600�b長の電線（同軸ケーブル）で電気的に結び、電源から、周波数が1MHz（＝10⁶Hz、波長が300�b）の交流（0.5V/-0.5Vのサイン波)を流し、600�b先の電圧測定器で、流れて来た電流を測定すると次の「測定結果：1」を得ます。 

 

 

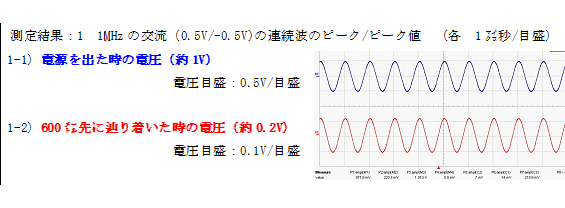　このように、1MHzの交流（0.5V/-0.5V）を、600�bの同軸ケーブル（電線）を流すと、その約5分の一(0.1V/-0.1V)に減衰してしまうのです。

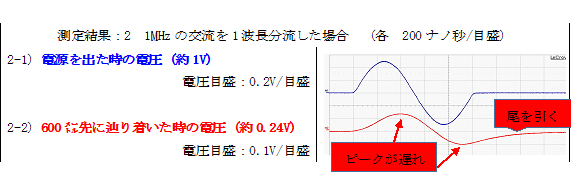
更には、同じ交流を1パルス（1波長分）のみ流した次の「実験結果：2」をご覧ください。

 

 

（両波形の相違が分かり易いように、時間軸の目盛を5倍にして表示しました）

 

測定結果中に書き込みましたが、「ピーク位置が遅れ」と共に「マイナスの波形が尾を引いて」おります上に、
「プラスとマイナスの最高値の高さがプラスの方が大」で、
更に、1波長分が時間的に引き延ばされ変形された形状となっております。

 

このような現象は、誤解された存在である「表皮効果」では説明不可能です。

そして、同じ時間軸の目盛で連続波の「測定結果：3」を次に掲げます。

 

 

　「測定結果：2」に見ますように、1波形分では、全く変形した波形を連続波として合算しますと、（当然ながら）この測定結果は「測定結果：1」と同様となります。

 

　そして、この「測定結果：1＆3」に見る「送電された減少された電圧波形」の裏側には、今回の「測定結果：2」の現象が隠されていたのです。

（ダジャレ的に表現しますと、誤解の存在である「表皮効果」に対して、「裏秘効果」となります）

 

しかし、実態は、導体（電線）中に存在する電気抵抗（抵抗）に起因する「多重反射現象」の結果なのです。

この件の詳細は、「新『コロンブスの電磁気学』（第6巻) 　交流理論は砂上の楼閣」或いは、『コロンブスの電磁気学』（新増補改訂版 カラー版 第1巻）をご参照下さい。

 

　因みに、今回使用しました600�b長の電線（同軸ケーブル）の抵抗値を実測しますと77.4Ωでした。

そこで、いわゆる一般的に抵抗による電圧変化を算出する「オームの法則」を使用しますと、電圧測定器（オシロスコープ）で測定されるべき電圧は、約0.56ボルトと算出されます。

　
　この計算結果は、先の測定結果の、0.2ボルトより遥かに大きな値ですが、
その0.2ボルトと出た「測定結果：2」の1波長分が時間的に引き延ばされ変形された形状となっている電圧波形（赤色線）を左側を固定して、
右から左へと押し付けてゆくと、計算結果である0.56ボルトに近い値となるでしょう。

この波形変形の結果、計算値と測定値に差が生じるのです。
そして、その差分が「多重反射現象」の結果（ダジャレ的には「裏秘効果」）なのです。
（多重反射の結果、電源側へと逆流してしまう電流も存在します）。