第13話

トランスの理論も誤解です

2016年6月11日　宇佐美　保

インターネットを見ますと、“環境、経済、平和などの、さまざまなNGO活動に関わる”と自己紹介されている田中優氏は、次の見解を披露されております。

 

同じトランスにつながっている家庭は5～10軒なので　田中優

 

今の送電線では役立てられない 　では家庭や地域にある低圧線に接続する小規模な発電はどうなるのか。 　実際には同じトランスにつながっている家庭は5～10軒なので、トランスの手前で他の家庭に流れていく。しかし低圧なので送電ロスは大きい。しかも家庭は太陽光の発電する日中は、休日以外は不在が多い上に消費電力もきわめて少ない。 　ではトランスを超えた電気はどうなっているだろうか。トランスはコイルを巻いた軸が互いに向かい合っている構造だ。そこではどちらからでも電気は流れる。 しかし困ったことに、この向かい合ったコイルを超えるときに周波数が90度ずれるのだ。   　すると周波数のずれた電気は「無効電流」となり、潤滑油の役割はするものの仕事をする力にならない電気になる。使えないのだ。最初から90度ずれることを見越した電気を流したらどうか。すると今度は近隣に流れる電気の方が無効電流になってしまう。結局、近隣でしか使えないのだ。   　結果として厳密なデータはないが、半分程度しか使えていないだろうというのが 現場の人の話だ。

 

　ここに見る、田中氏の”しかし低圧なので送電ロスは大きい”とのご見解は、「送電ロスは電線の抵抗に起因」との現在の電気理論に基づいています。
しかし、「交流送電の伝送ロス」は、「電線の抵抗起因」だけではないのです。
この件は、是非とも拙著『コロンブスの電磁気学』（新増補改訂 カラー版 第1巻）の『補足編　第10章　第6節　交流送電の問題点』をご参照下さい。

更には”向かい合ったコイルを超えるときに周波数が90度ずれる”とのご見解は、一般的なトランス理論（ファラデーの電磁誘導の法則）で語っており、実際に実験してみれば、全く的外れなご見解であることがすぐに判明します。

　従来のトランス動作原理が「ファラデーの電磁誘導の法則（式：1）」であるならば、

式：1

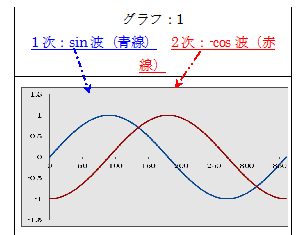
次に掲げた「グラフ：1」のように、トランスの1次側コイルへのサイン波（sinωt）を入力した場合は、2次側コイルでは、サイン波の微分波形である‐コサイン波、即ち、1次側のサイン波より位相が90度遅れたsin波を観測して然るべきです。

 

この件を確認する為に、トランスの1次側コイルへ入力信号をサイン波の連続波、並びに、1パルスのみとして、1次側入力電圧波形、2次側への出力電圧波形を同時に測定すれば、「グラフ：1」の関係が得られる筈です。

 

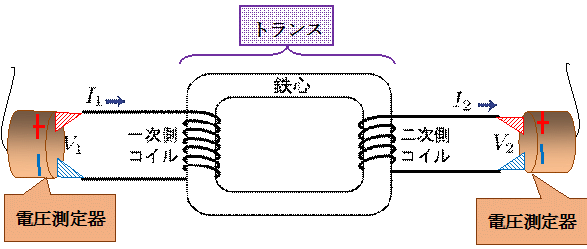
そこで、通常の家庭用の電気である周波数が50Hzの交流電流を（電圧は、測定機器の都合で1ボルトとしました）、市販のトランスの1次側に入力して、そのトランスからの出力信号（2次側の電流）を、各々電圧測定器（差動プローブ）を用いて次の「図：1」のようにして測定しました。

図：1

 

 その結果は、次の「測定結果：1」に見ますように、「ファラデーの電磁誘導の法則（式：1）」から得られる、「1次側と2次側の電流の位相が90°ずれている波形」ではなく、同位相の波形を実測結果として得るのです。

 

 

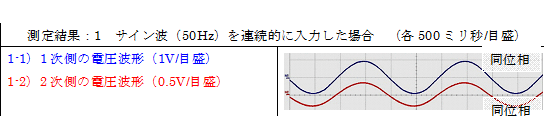この実測結果から、トランスの動作原理は、従来固く信じられている「ファラデーの電磁誘導の法則（式：1）」でないことが明らかとなります。

 

それでも、念に念を入れ、矩形波信号（1V/0V）を1パルス（1波形：恰も羊羹の一切れのような形状をした波形の信号）を同じトランスの1次側に入力して、先の「図：1」の状態で、「測定結果：1」を得たと同じように測定して、次の「測定結果：2」を得ます。

 

この際、矩形波信号の周波数（いわば、羊羹の長さ相当）を、0.1Hz、10 Hz、50 Hz、250 Hz、500 Hzと、 変化させました。

 

 

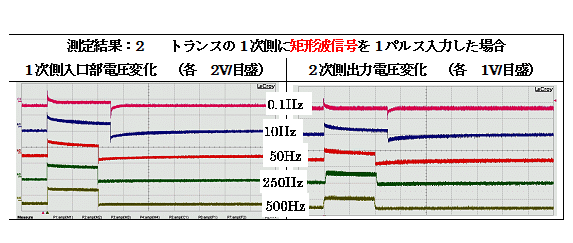　この測定結果をみて、矩形波信号（いわば、羊羹状の四辺形の波形）を、トランスの1次側に入力したのに、測定結果では、次の3点を見て驚き、従来のトラン理論が完全に崩壊します。

　ここで、『第6話　交流も直流も同じ電気（電気は近接作用）』を思い出してください。

そこで、前掲の「測定結果：2」を、時間軸の単位を同じ目盛（1目盛を500マイクロ秒）に統一して「測定結果：3」として、更に、それらの結果を重ね合わせて「測定結果：4」として、次に表示します。

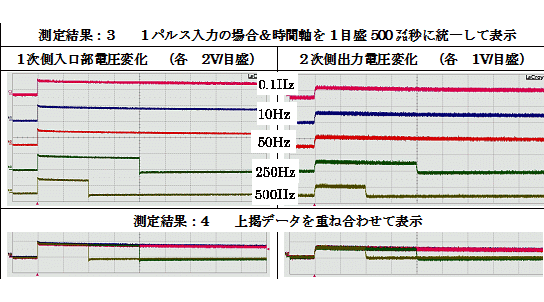この結果からご納得頂けますように、「羊羹」一切れを入力している際、トランスはその「羊羹」一切れがどのくらいの長さかは、全部入力されてから分かるのであって、「羊羹」が一切れ分全部トランスに入力されてから、トランスは2次側に出力するのではありません。
そして、『第6話　交流も直流も同じ電気（電気は近接作用）』の目をつぶったままパンチを受けていると同様に、この際、トランスは、目をつぶったまま、羊羹を口に押し込まれている状態です。
従って、トランスの口は、その先のことなどわからず、どんどん押し込まれてくる羊羹に対処するだけです。
押し込まれる量が増えるにしたがって、口からはみ出してしまい、一部しか口の中へ入って行きません。

 

　ですから、ここでの測定で、一切れが一番長い「羊羹」（0.1Hz）を口にしているつもりでも、途中で、「羊羹」の長さがそんなに長くない（例えば、10Hz、或いは、50Hz、はたまた、250Hzと短い）と気が付いても、いわんやこの場合で、一番短い一切れ（500Hzの長さ）でしかなかったとトランスが、気が付いても、それらの「羊羹」に同じように応対しているのです。

　では、交流の場合は？と申しますと、勿論、この直流の場合と同じです。
ただトランスの口に押し込まれてくる「羊羹」の形状が、直方体ではなく、「鰹節」のような「紡錘形」をした「羊羹」と考えられます。
この件は、次の『トランスの理論も誤解です（交流編）』をご参照ください。

 　尚、”それでは、トランスの理論は「ファラデーの電磁誘導の方程式」に基づかないなら、どんな理論がある！？”と、お思い頂きましたら、拙著「新『コロンブスの電磁気学』（第5巻） 新たなトランス理論」、或いは、「『コロンブスの電磁気学』（新装改訂カラー版 第1巻）」をご高覧頂きたく存じます。