『コロンブスの電磁気学』の要旨（16）　クロック信号の本質（2）

2011年4月2日

宇佐美　保

　前の≪『コロンブスの電磁気学』の要旨（15）　クロック信号の本質≫の「測定結果：1＆2」に於いて、単独の1パルス波を4個連続的に加算する状況が分かりにくかったかもしれませんので、今回はその測定結果画面（即ち、オシロスコープ画面）の様相を変えて表示しました。

　尚、前回の各クロック信号の出力は、1V/0V　でしたが、今回は、500mV/0V　として、先と同様にコンデンサからの出力波形を差動プローブにて測定いたしました。

 

　又、測定したクロック信号の周波数、周期＆1パルスの発信時間を、次表に纏めて表記いたします。

 

表：1
周波数	周期	発信時間（＝周期/2）	発信時間×4
100MHz	10ns	5ns	20ns
25MHz	40ns	20ns	80ns
6.25MHz	160ns	80ns	320ns
1.563MHz	640ns	320ns	1280ns
390.6KHz	2560ns	1280ns	5120ns

 

 この表に表記された周波数の1パルスのクロック信号の「発信時間×4」の値が、それより一段下の欄に表記された1パルスのクロック信号の「発信時間」の値が同一であることは、直ぐにお分かり頂けると存じます。

そしてこのような関係にある1パルスのクロック信号を用いて前文同様な測定、即ち4個の単独パルスによる出力波形を、その発信時間置きに連続して配置しそれらを合算し、それらの「発信時間×4」に等しい「発信時間」を有する1パルスのクロック信号による出力波形とを比較しました。

以下の測定結果は、100MHzと25MHzの組み合わせの場合を始めとして順次表示しました。

 

　ここでの各単独パルスの測定結果の内、第1番目のパルスの出力結果は青色、それ以降、赤色、緑色、茶色と続いております。

　

このような過程を経て、以下の測定結果は、100MHzと25MHzの組み合わせの場合を始めとして順次表示しました。

　そして、これら4個のパルス波による出力結果の合算波形と、それに相応する1パルスによる出力波形を同一画面に近接させて表示して、両者が同一波形になる事を確認しました。

測定結果：1

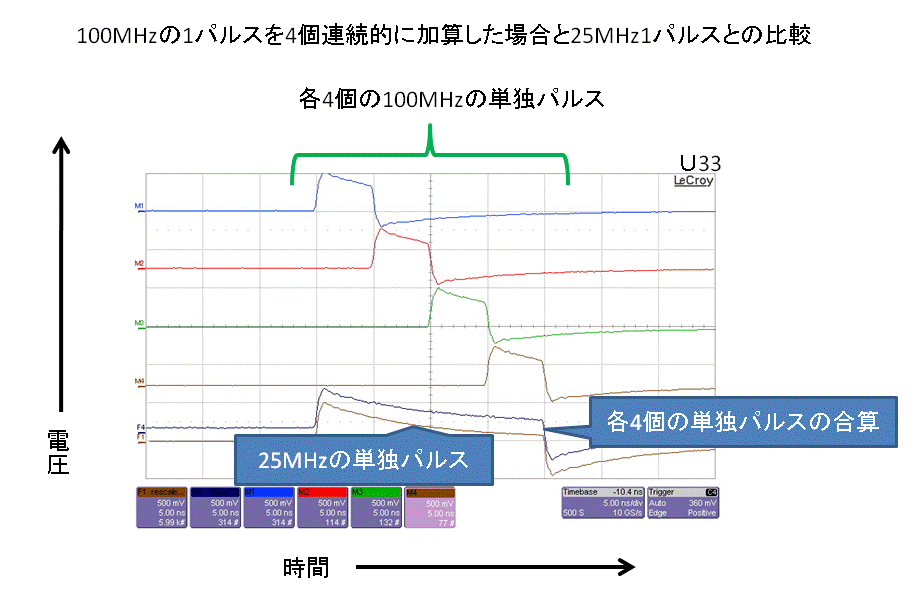測定結果：2

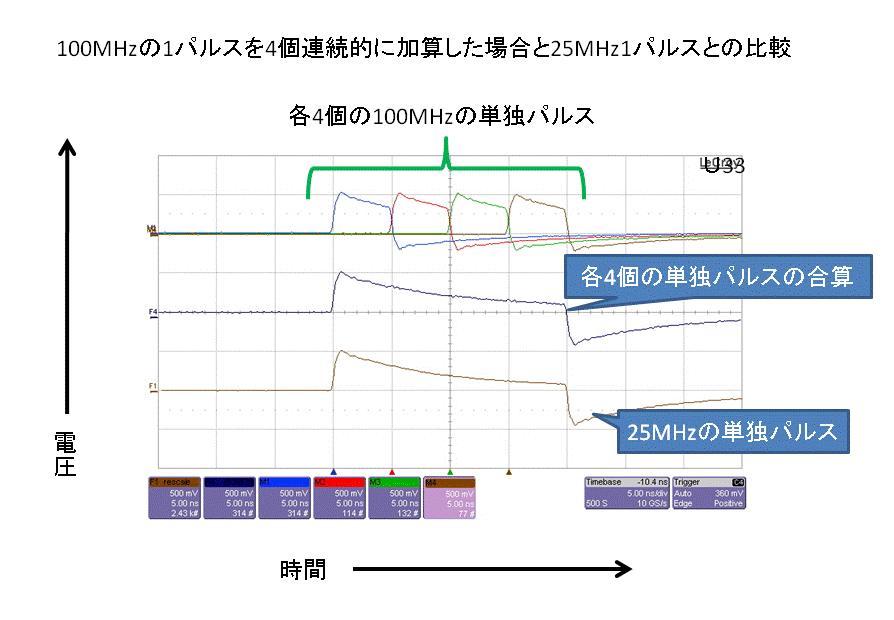測定結果：3

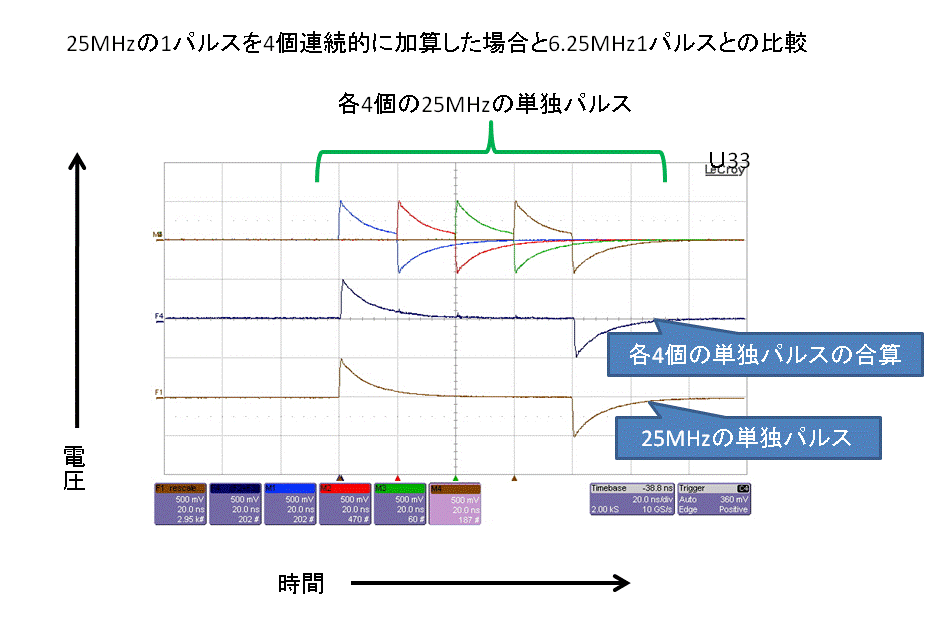測定結果：4

 

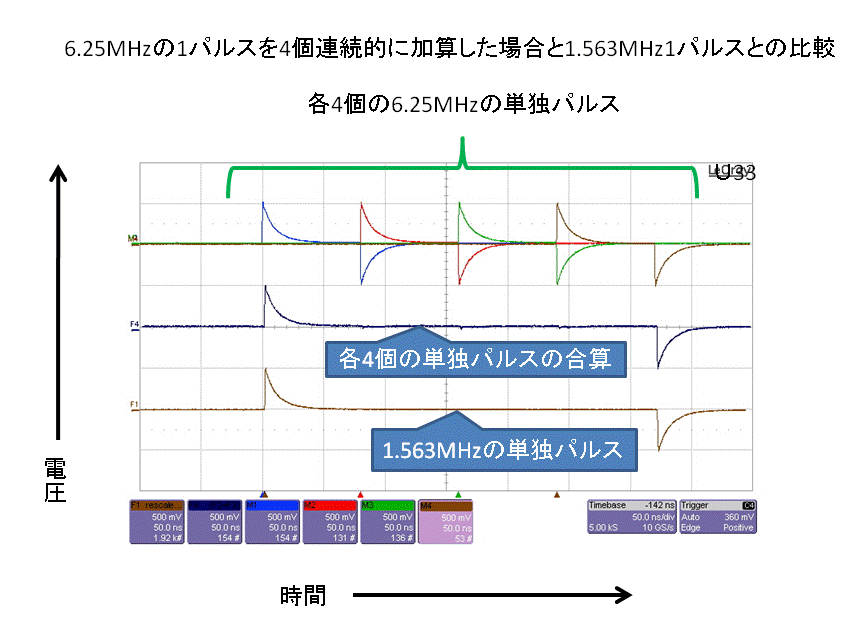これらの結果を見ますと、「測定結果：2〜4」は、前回同様、クロック信号が単独波の集合体であろうと単独波の1波であろうと、それらの信号の発信時間（前者の場合は合算値）が同一であれば、前回同様に、出力結果も同一になる事が確認されます。

　この結果の内、「測定結果：4＆5」の単独波の出力波形は、ゼロボルト部分が続いていますから、コンデンサ内の電圧が飽和状態になっている事が分かります。

 

このような状態に関しては、先の≪敬愛するマイケル・ファラデー（7）　縦列接合がコンデンサの謎を解く≫の、「イメージ図：10」を再掲いたします。

 

縦列結合……の「イメージ図：10」

　

　この「イメージ図：10」に見ますように、コンデンサ内の電圧が飽和状態になった後に、入力信号がオフ状態になりますと、コンデンサからの出力波形は、信号入力時の出力波形と正負対称形の同一波形である事が分かります。

 

　従いまして、「測定結果：4＆5」に於いて、第1単独波のオフ時の出力波形は、第2波のオン時の出力波形によって相殺されます。

又、この第2波のオフ時の出力波形は、第3波のオン時の出力波形によって、相第3波のそれは第4波のそれで殺されます。

（尚、私が使用しているオシロスコープの1画面で見る事が出来るメモリー波形は4個だけなので、ここまでの測定結果は4個の単独波を合成していますが、単独波が4個以上何個続いても、それらのオフ時の波は、それに続く波のオン時の波によって相殺され続けます）

 

　この事から当然、390.6KHzよりも低い周波数の信号に関しても、「測定結果：4＆5」と同様な測定結果が期待されます。

 

　更に、「測定結果：2＆3」のように、コンデンサ内の電圧が飽和状態になる前に、入力信号がオフ状態になってしまう場合を考察します。

この場合も、先の≪敬愛するマイケル・ファラデー（7）　縦列接合がコンデンサの謎を解く≫の、「イメージ図：8＆9」等に見ますように、第N番目の単独波信号がオフになった場合の、コンデンサからの出力信号の変化としては、先ず、入力伝送路から出力伝送路への直接的な（プラス）出力が消え、その次は、コンデンサ内の第1次反射分の（マイナス）出力、そして、第2次反射分の（マイナス）出力……とが順次消えて行きます。

そして、この変化は当然、コンデンサ伝送路内を電流が往復する時間ごとに発生して行きます。

 

　一方、次の第（N+1）番目の単独波をオンしますと、先ずは、入力伝送路から出力伝送路への直接的な（プラス）出力が発生し、その次は、コンデンサ内の第1次反射分の（マイナス）出力、そして、第2次反射分の（マイナス）出力……とが順次、コンデンサ伝送路内を電流が往復する時間ごとに発生して行きます。

 

　この結果、第N番目の単独波のオフ効果は、第（N+1）番目の単独波のオン効果によって完全に相殺されます。

 

　従って、第N番目の単独波、並び、第（N+1）番目の単独波が継続されて入力されていた状態と等価となります。

勿論、第（N+2）番目、第（N+3）番目……と続き手も同様な結果が得られます。

 

（そして、この考察は当然ながら「測定結果：3＆4」のコンデンサ内の電圧が飽和状態になった後での、単独波のオン/オフの場合に関しても適用されます）

 

　以上を考慮して、改めて、「表：1」更には「測定結果：2〜5」を見ますと、390.6KHzの1パルスのクロック信号は、100MHzのクロック信号を（発信部分を連続させて）256個つなぎ合わせた合成信号と等価である事が分かります。

 

　そして、この事象は逆に辿れば、390.6KHzの1パルスのクロック信号が、100MHzずつのクロック信号の集合体（256個分）に留まらず、更に細分化して行く事が可能と考えられます。

　例えば、この100MHzのクロック信号は、400MHzのクロック信号の発信部分を４個合体した信号に相当するはずです。

この点を次に確認しましょう。

即ち、此処までの測定方法で、100MHzと400MHzに関して比較した結果を、次の「測定結果：６」に掲げます。

 

測定結果：６

 

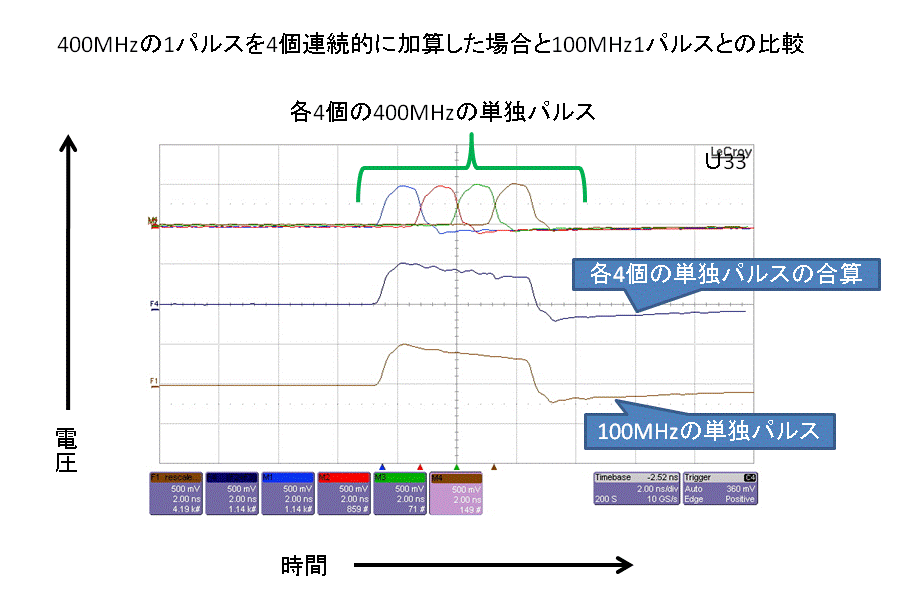更には、400MHzは、同様に1.6GHzの細分化とみなされ、そして、最終的にはもうこれ以上細分化できない「量子的」な単位にまで細分化されるでしょう。

　この事は、前文の「概念図：1」から「概念図：2」への変換が改めて正当化されるのです。

（即ち、“クロック信号は、量子的電気の集合体”との解釈の正当性）

 

　その上、前文では、出力は1V/0Vで以上の点が正当化され、今回は、500mV/0Vで正当化されました。

 

この事は、時間的な細分化同様に、電圧的な細分化も可能と考えられます。

 

その結果、次の概念図を想定する事が可能です。

クロック信号の概念図

 

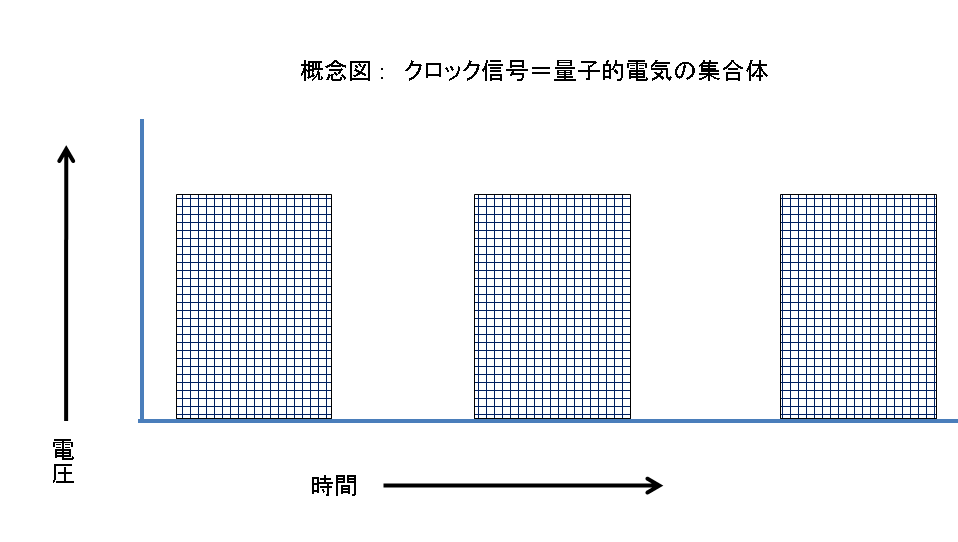（勿論、この細分化は、クロック信号に限らず、全ての電気信号に対して可能であることは言うまでもありません）

 

そして前文同様に次のように考えられます。

電池に於ける電気発生を微細に見れば、電池の両電極に於ける電子レベルの反応です。

 

　ですから、この「量子的な電気（電磁波並びに光）が、粒子的に振る舞い」、「量子的な電気（電磁波並びに光）の集合体が、波として振舞う」のだと存じます。

 

　この結語は、『コロンブスの電磁気学』増補改訂版の「第2章　第1項　電気とは？」の結語であり又、次のようにも記しております。

（この件は、『第16章　第4項　最小単位の電気に基づく伝送特性の考察』を是非とも、ご参照ください）

 

 

　是非とも、『コロンブスの電磁気学』増補改訂版を御目通し頂きたく存じます。

そして、次の≪『コロンブスの電磁気学』の要旨（17）直流も交流も量子的電気の集合体≫に移らせて頂きます。