| 第10話 |
ファラデーの電磁誘導の法則は誤解です(1)
2016年6月6日 宇佐美 保
「ファラデーの電磁誘導の法則：コイル内に発生する起電力Vは、そのコイルを貫く磁束φの時間的変化に比例する」こそが、発電の原理であると、どなたも信じて疑わないと存じます。
（注）ファラデーの電磁誘導の法則の数式
 |
（式：1） |
但し、kは比例定数、又、一連の拙著では磁束を磁界と表記しております。
しかし、おかしいではありませんか！？
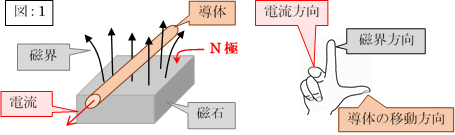
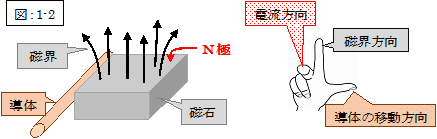
私達は学校で「発電現象」に関して、次の「図：1」のような「フレミングの右手の法則」を教わって来ました。
| 「フレミングの右手の法則」 （図に於ける導体と磁石の相対的移動は左右方向） |
 |
但し、この場合は連続的な発電現象ではありませんので、次の「写真：1」のように、1本の導体（コの字型に曲げた銅棒（直径：3mm））の回転によって「フレミングの右手の法則」通りに「連続的な発電結果」を確保できるのです。
 |
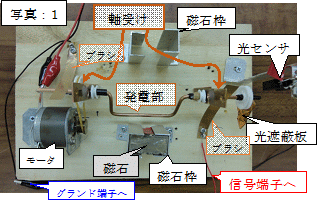尚、「コの字型銅棒部分」を磁界内でモータを用いて回転させますが、その回転方向は、右の軸受け側から見て、時計方向の回転とし、「銅棒の発電部分（コの字型部分）」と共に回転する「光遮蔽板」が「フォトインタラプタ（光センサ）」の光を遮る事で、「コの字型銅棒部分」の存在位置が検出されるようにしました。
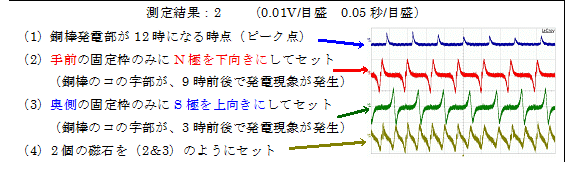
この「発電機」にて、次のように、磁石（30mm角、厚さ：15mmのネオジウム磁石）の設置（アルミ製の枠で固定）方法を変えて「測定結果：1」を得ました。
 |
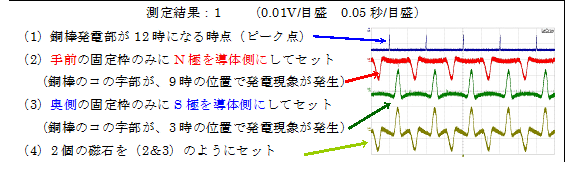この結果に見ますように、「ファラデーの電磁誘導の法則（磁束規則）」とは無関係に、ループ（コイル）を形成しない「1本の導体」での発電が可能です。
当然ながら、各場合とも発電現象は、「コの字型銅棒部分」が磁石に最も近付いた時、即ち、結果（2）の場合は、銅棒が（位置の検出モニターに対して）9時の位置、（3）の場合は、銅棒が3時の位置で最も顕著に認められます）
そして、そこでの発電状況は次の「図：2」に見ますように、「フレミングの右手の法則」そのものです。
 |
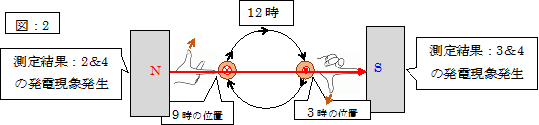更に（4）はその両者の合算（測定結果：2-2のグラフと、測定結果：2-3のグラフを重ね合わせた状態）であり、日頃、コイルを磁石間で回転した場合に得られる発電状況そのものです。
即ち、この1本の銅の丸棒の回転によっても、従来“閉回路内の磁束の変化に応じて閉回路に電流が発生する”と信じられてきた“コイル（閉回路）を回転した場合と同様な発電結果”が得られるのです。
（繰り返して記述しますが、それも、よく知られている発電に関する「フレミングの右手の法則」通りの結果となっているのです）
ところが、発電の原理は「フレミングの右手の法則」に合致しない場合、即ち、「図：1」の導体が磁石の横の位置に存在する場合にも、発電現象が発生することを、先の『第10話 食塩水も銅線も同一発電現象』の「測定結果：1」に見るのです。
| 「フレミングの右手の法則」に合致しない場合 （図に於ける導体と磁石の相対的移動は上下方向） |
 |
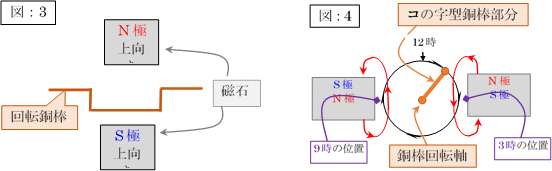
そこで、この場合も先の「測定結果：1」を得た場合同様に、次の「図：3＆4」のように、「コの字型銅棒部分」に対して、N極/S極を上下に向けてセットして、この場合も「測定結果：2」の連続的な発電結果を得るのです。
 |
 |
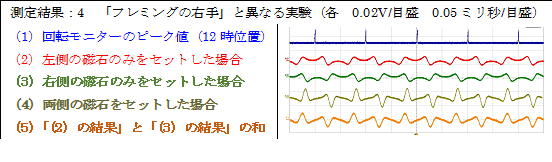
次には、ポリプロピレン（PP)の枠（各辺の寸法は、幅：2cm、長さ：4cm）にエナメル線を20回巻き付けたコイルを作成して「測定結果：1＆2」を得たと同様な実験を行い、各々「測定結果：3＆4」を得ました。
 |
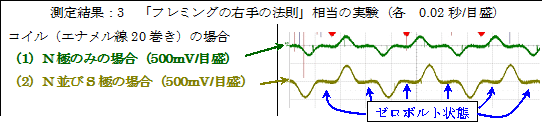この実験は、磁石の前でコイルを回転しているのですから「ファラデーの電磁誘導の法則」に従って当然と思える状態ですが、
上の測定結果のようなゼロボルト状態は、「ファラデーの電磁誘導の法則」では説明できません。
（何故なら、磁界の中で回転するコイルを貫く磁界の量の変化が、長い期間にわたりゼロとなることはありません、
従って（式：1）から、発電電圧が、長い期間にわたりゼロとなることはありません）
 |
如何でしょうか？「ファラデーの電磁誘導の法則」をまだ信じますか！？
次話では、発電原理は「ファラデーの電磁誘導の法則」に関係ない事を更に証明します。