物理学者もアインシュタインの相対性理論を誤解します
2000年5月14日
宇佐美 保
目次
1:「序」と『ガリレイの相対性原理』
2:光の世界
3:双子のパラドックス
4:紐で結んだ2台のロケットのパラドックス
5:「ガレージのパラドックス」
6:ミユー粒子(ミユー(〃)オン)の寿命
7:ミユー粒子(ミユー(〃)オン)の寿命の
8:「固有時間」を用いての解釈
9:“双子のバラドックス”に対しての「固有時間」を用いての解釈
10:「?の時間」は「空間の時間」
11:実際には、どちらの双子が年を取ったか?
12:ミユー粒子の寿命で具体的に考えましょう
13:夢の中での天国のアインシュタインのお話
(補足:1):回転時空図で『双子のパラドックチ』を考えてみましょう。
(補足:2):赤道上と南北の極に置いた時計の相違は?
(補足:3)「特殊相対論」と「一般相対論」
(お断り:引用文中の下線、網掛け、着色処理等は私が施しました)
1.)「序」と『ガリレイの相対性原理』
先ずは、私の昔話から始めます。
東京に都電が走っていた頃、私が小学生だった頃の話です。
小学校六年の最後の授業に、担任の先生が言われました。
「最後の授業を終るに際して、今までの授業の中で、又、授業以外で皆さんが、判らなかった事、不思議に思った事がありましたら、手を上げて下さい。先生が答えますから。」
其処で、“これで、永い間不思議に思っていた謎が解ける”と思い、私は喜び勇んで手を上げました。
「先生!何故電車の中で、物を落すと、落した物が電車の後ろの方へ飛んで行かないで、何故自分の足元に落ちるのですか?」
「それは宇佐美君、電車のスピードが遅いからでしょうよ。君が何時も乗っている都電のスピードが遅いから、足元に落ちるように見えるだけで、もっと速い電車だったら、落下物は後ろの方へ落ちるでしょうよ。」
「先生、でも、もっと速い電車でも足元に落ちるのです。遠足に行った時も、同じ事を試してみるのですが、いつも足元に落ちるのです。靴を落したり、石を落したり、紙を丸めて落したり、色々試してみたのですが、いつも足元に落ちるのです。」
「それは、宇佐美君が何か勘違いしていたのではないですか?」
周りの皆んなも、先生に同調して、「そうだよ、そうだよ、宇佐ちゃん何寝言云ってんだよ!」と野次り出しました。
なにしろ、当時の私には、小学校は勉強に行く為に存在するのでなく、みんなと一緒に騒いだり、特に野球をする為に行く場所だったので、私は、ホームルームの時間には、何度か吊るし上げられたりしていたのです。
「宇佐ちゃんは、教科書も帳面もみんな学校の机に置きっぱなしで家に持ち帰らないので宿題もしないのです。」とか、
「宇佐ちゃんは、骨折が何ヶ月も前に直っていたのに、学校へ来ないで近所の小さい子を集めて野球して遊んでたのです。」といった具合ですから、友達も先生も、私の疑問を真面目に受け止めてくれなかったのでしょう。
そして、後年、『慣性の法則』(下記の「平凡社の百科事典」からの抜粋を御参照下さい)
| 外部から力の作用を受けない物体は,初めに静止していればそのまま静止を続け,初めにある速度をもっていればその速度を保持して等速度運動を続ける。この性質を慣性と呼ぶ。このことを法則の形ではっきり述べたのがニュートンの運動の第1法則であり,それは慣性の法則とも呼ばれる。 |
を知る事で、私の小学生以来の謎が氷解したのです。
なのに、十年ほど前、高校時代の友人にこの話をしたら、友人は「宇佐美君、電車の外へ落せば、物は、電車の後ろに落ちたのに。」と真面目くさって言いました。
ですから、私の友人のように、電車と、電車に乗った私の手の中の小石についてのお互いの速度を比較する際に、電車には、モータが付いていて、小石にはモータも何も付いていない点等で、頭の中が混乱される方も居られますので、ここで、『慣性の法則』ての説明を付け加えさせて頂きます。
一直線のレール上で、電車がモータの力を借りて十分なスピードを出して、モータの働きを切ってしまった状態を考えて下さい。
この状態で、車軸の摩擦やレールとの摩擦などが無い限り、電車は、何処までも真直ぐに走り続けるでしょう。
即ち、“外部から力の作用を受けない(モータの働きを切って、車軸の摩擦やレールとの摩擦などが無い)物体(電車)は”“等速度運動を続ける(何処までも真直ぐに走り続ける)。”
そして、更に、電車に乗った私達も、私達の手の中の小石も、電車がモータの働きを切った時点では、電車と同じスピードで前方へ移動し続けているのです。
ですから、電車がモータの働きを切っても、電車と同じスピードで前方へ走り(移動し)続けるのです。
その結果、電車の中の私達がジャンプしても、電車の中のもとの位置に着地しますし、手の中の小石を落しても足元に落ちるのです。
(しかし、電車の中の空気は一緒に移動していますが、電車の外(電車の中といっても、電車の囲いの無い場合、例えば、オープンカーの如き場合)の空気は、電車と一緒のスピードで、電車と一緒に前方へ移動していませんので、その空気(風)の影響で、私達の髪の毛が後ろに靡く様に、丸めた紙などは、後ろに飛ばされたりしてしまうのです。)
そして、この事は、電車に限らず、もっとスピードの速い、新幹線でも、ジェット機でも、同じなのです。
なにしろ、私達の地球は、太陽を「秒速約30キロ・メートル(この速度では、月までは3時間半ほどで行けます)」のスピードで周っているのです。
(下記を御参照下さい。)
|
太陽からの距離 最小=1.471×108km 平均=1.496×108km 最大=1.521×108km 公転周期=365.256日 平均軌道速度=29.78km/s 地球の中心と月の中心との間の平均距離は38万4400km |
それでも、こんな速いスピードで動いている地球に乗っている私達が、地球上でジャンプしたり、物を落しても、元のところに降りてくるのは、今まで述べてきた電車の中の出来事と全く同じ事なのです。
更に、話を続けますと、走っている車から小石を落すのでなく、前方へ投げれば、小石のスピードは、車のスピードが加算されたスピードで前方に飛んで行きます。
これは、私達の常識であります。
このような、常識が成り立つ世界を、『ガリレイの相対性原理』が成り立つ世界と言うのです。
若しもこの常識が、通用しなかったら大変な事です。
例えば、時速約300キロメートルで走る新幹線の中でキャッチボールをしたら(こんな事は許されないのですが)現在日本一の球速(時速155キロメートル)を誇る松坂投手でも、前方へボールを投げる事が出来なくなってしまうのです。
なにしろ、松坂投手の投げるボールのスピードよりも、新幹線のスピードの方が速いのですから。
(それに、物騒な事に、300-150=時速145キロメートルのスピードで後部へボールが飛び去ってしまうのです。)
それどころか、新幹線の中を前方に移動しようとしたら、時速約300キロメートル以上のスピードで歩かなくてはなりません。
これでは、何の為に新幹線に乗るのか判らなくなってしまいます。
それに、手から落した小石が列車の後ろ方向へ飛んでいってしまうのは勿論、私達は、ジャンプしたら、私達の体は列車の後ろ方向へ飛んでいってしまうでしょう。
(電車のスピードが加味されてなくては、停止している私達の体や、小石のスピードは、秒速0メートルなのですから、電車に置き去りにされてしまうのです。)
それどころか、秒速約30キロ・メートルで移動する地球から、私達は振り落とされてしまいます。
2.)光の世界
そして、光の世界は違うのです。
『ガリレイの相対性原理』を拒絶する世界なのです。
『アインシュタインの相対性理論』の世界なのです。
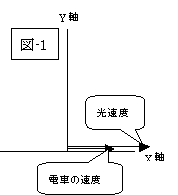
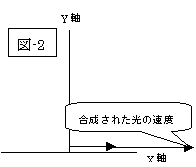
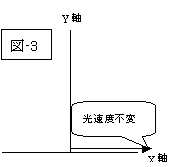
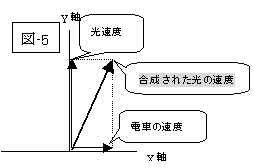
走っている車から前方へ光を発射しても、光のスピードは不変である、即ち、「光速度不変」が『特殊相対性理論』の土台なのですから、『アインシュタインの相対性理論』その出発点からして私の頭を混乱させます。
ですから私達が、中学生或いは、高校生のとき習った速度の合成方法が通用しないのです。
| 『ガリレイの相対性原理』の世界 | 『アインシュタインの相対性理論』の世界 | |
 |
 |
 |
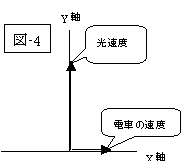
従って、
| 『ガリレイの相対性原理』の世界 | 『アインシュタインの相対性理論』の世界 | |
 |
 |
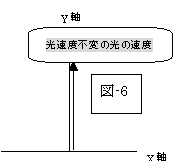 |
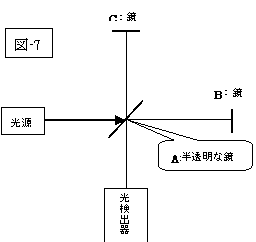
この『アインシュタインの相対性理論』での「光速度不変」の世界で、次図に示す有名な『マイケルソン・モーレーの実験』を解釈するのが難しくなります。
 |
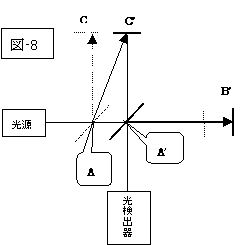 |
前図、(図-7)(図-8)において、この装置全体が、地球表面に(図の右が地球の公転方向(公転速度:秒速約30万キロメートル)に相当するように)置かれ、光源からレーザー光を半透明な鏡(A)に向けて発射すると、装置全体は地球の公転につれて運動しているのですから、『アインシュタインの相対性理論』に従いますと、Aの鏡を通過してB鏡へ行く光は、「光速度」は、(図-3)の通りに、不変で又、進行方向も継続して、鏡の位置B’迄行き反射される事にはなりましょうが、Aの鏡で反射されてCの鏡へ行く光は、(図-6)に従うなら、(図-8)の(「実線の矢印方向」でなく)「点線の矢印方向」に進んでしまい、光がCの鏡についた時点には、すでに鏡は地球の公転速度に従って、C’の位置に移行してしまっていて、鏡に当たる事が出来ず、反射されないのではないか?との疑念を抱いてしまうのです。
そして、この疑問を起点として、『アインシュタインの相対性理論は間違っている!』と論を進めた本を見かけたことがあります。
そこで、私の頭の中をすっきりさせたいと思い、『時空図で理解する相対性理論』(和田純夫著:1998.12.10:ナツメ社発行)を購入して読んでみました。
すると、67頁〜73頁に、走っている電車の中の鏡による光の反射の事例で、「時間」を観測する人が、「電車の中か外に居るかの相違」で、「観測される時間にズレが生じる」事を説明していました。
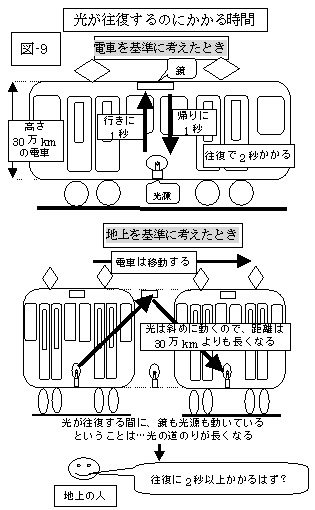
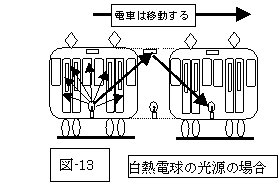
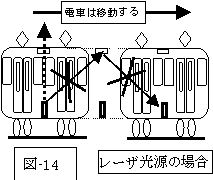
しかし、この本の説明では、光源に白熱電燈を用いています。ですから、下図の如くに、真上にも、電車の進行方向の斜めにも光は放射されるので、下図(図-9、10)の如きの説明が可能でしょうが、光源としてレーザー光を用いたらどうなるのでしょう?
 |
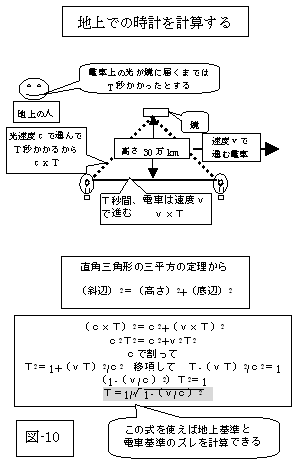 |
電車に乗ってる人が、電車の真上にある鏡に向けてレーザー光を発射したら、どうなるのでしょうか?
レーザー光は、鏡に当らないのでしょうか?
それとも、電車に乗ってる人は、レーザー光が鏡に当るのを目撃して、電車の外の人は、レーザー光が鏡から外れるのを目撃するのでしょうか?
この疑問を解消したいが為に、『なっとくする相対性理論』(松田卓也、二間瀬敏史共著:1999.7.10:講談社サイエンティフック発行)を更に、購入しました。
と申しますのは、この本の著者の松田氏が、本稿の冒頭に書きました私の体験と似た(中学生の時、海水浴へ行く列車の中で、爪切りを落として私と同じような)体験をなさったと、書かれていましたことと、下記に掲げましたような、「前書き」に興味をそそられたからであります。
相対論の教科書のオンパレード
講談社から「なっとくする相対性理論」という題で本を書いてほしいと頼まれたときは,正直いって躊躇した。
|
相対論に関する本はそれほど掃いて捨てるほどある。…… しかし,本の棚を見るうちに,相対論は間違っているとか,ビッグバン宇宙論はウソである,といった一群の本が目についた。内容を一瞥すると,内容の疑わしい疑似科学の本であることはすぐにわかった。しかしそれらの本の著者たちの中には,いっぱしの大学教授たちもいるのである。おやおや。私達もそのはしくれではあるが,大学教授といってもさまぎまだなあと思う。もっとも大学教授だけあって,その論理は他の素人の論者の幼稚な論理よりは多少はまともであるが,明白に誤っていることに変わりはない。 くだんの教授たちは,相対論の専門家でないどころか,物理学の専門家でもないというのが,一つの特徴であることにも気がついた。それら疑似科学本の著者たちは,その意味ですべて素人である。もっとも素人までが相対論に関して発言するというこの現象は,相対論が賛成・反対を問わずいかに人気があるかということの反映であろう。一方,量子論ではそのようなことはあまりない。量子論が抽象的すぎて難しいからであろう。 …… こういったことが趣味ですんでいる間はよい。しかし,明白に誤った本が堂々と書店で売られるとなると,弊害も発生する。…… 出版社としても,いいかげんな本を出版すると,信用が損なわれるからである。それが最近はある程度名の知れた出版社から,これら疑似科学本が,多数出版されるという現象が起きている。そんな本ばかりを出すなら,それはそれでもいいだろう。しかしその出版社からは東大の著名な宇宙論,惑星科学の大家の本も出版されているから,一般の読者はこれら珍理論の本もそれなりの権威があると錯覚してしまうかもしれない。カンぐれば,出版社はそれが狙いなのかもしれもしれない。…… もちろん民主主義のこの世の中であるから,言論・出版の自由はある。 また資本主義社会であるから,出版社にとっては,本が売れればそれでよいのであろう。テレビは視聴率がとれれば,なにを放送してもよい,本屋は本が売れれば内容はどうでもいい。そんな世の中にわれわれは生きている。とにかく銭が儲かることは正義であるという風潮があるのである。 しかしこの風潮は、科学界でも多少は問題になり,池内阪大教授(現名古屋大学教授)は朝日新聞に抗議の一文を載せている。天文・天体若手夏の学校でも、この現象に抗議する分科会が持たれているのが現状だ。筆者も天文学会の一般教育分科会で講演を依頼され,喝采をあびた。…… 科学的トンデモ本にもさまざまある。著者も一人ではない。自分の理解できないような相対論・宇宙論は誤りだという粗雑な議論,相対論は常識に反するから誤りだという幼稚な議論,数学がまるでわかっていない初歩的な誤り,実にさまぎまである。なかには虚数や負数は存在しないという,本当にとんでもない議論まである。負数があるならマイナス百万円を見せろと,その著者は言う。それへの回答は簡単だ。私の銀行通帳を見てもらえばよいのである。 そもそも虚数がなければ高校の二次方程式も解けなくなるではないか。 電気回路では複素数はしょっちゅう出てくるし,量子力学の波動関数は複素数そのものだ。複素数を否定すれば,現代科学・技術が崩壊する。…… 本書の私の分担部分(第1章〜第4章)では,トンデモ本に紹介された特殊相対論に関する誤解を,ところどころ例に取り上げた。そうすれば,なにがしかの新味を加えることもできようし,初学者の陥りやすい過ちも指摘できると思ったからだ。 もっとも本書全部を疑似科学本への反論とする,というようなことはしない。そんなことはページの無駄である。…… |
この抜粋文中の「特殊相対性理論」を「宮沢賢治論」と置き換えて読むのも一興と思いましたので、一寸長い抜粋でしたが、ご容赦下さい。
しかし、残念ながら私の疑問を晴らしたくれるどころか、かえって疑問を増大してくれました。
先ほどの、電車の中の光源は、白熱電球のようでした。
それでは、ランプから四方八方へ光が飛び出すので、電車の中の人が、電車の真上に向かって光を投げかけても、それ以外にも電車の進行方向などへも光が放射されますから、電車の外にいる人は、電車の中の人が真上に向けて放った光でなく、電車の進行方向の斜め前方に向かっていろいろの角度で放射された光のうち、それら四方へ飛び出した電車の天井に届いた光のうち、たまたま、そこに電車の鏡が来ていた光が反射されるとも解釈されてしまいます
 |
 |
 |
 |
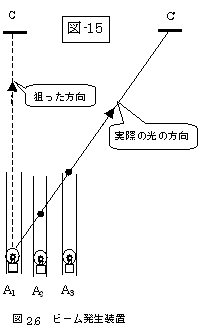
ところが、残念なことに、松田氏はレーザー光でなく、次図の如きの「光源の先に筒をつけたもの(ビーム発生装置)」なる光源で、以下のごとくに、説明されるのです。
(尚、松田氏の説明文は、上記の電車の中の光の話とは、状況が異なり、有名な「マイケルソン・モーレーの実験」に対してではありますが、論の進め方は、次の説明文、並び、図中(図-15)のAを電車の中の光源、Cを電車の天井の鏡として、上記の電車の中の光の進み方の説明と考えて差し支えないと私は判断いたしました。)
|
……中にはとんでもない誤解をする人もいるので,ひとこと注意しておきたい。その誤解とは次のようなものである。Aから出た光の先頭は,図2.5鏡Cのほうに行ってその間に鏡CがC′には行けば、反射することなく戻ってこない,というのである。 これはとんでもない誤った説だ。こんなバカげたことは,19世紀の学者たちも言っていない。そんな考えは,19世紀の学者たちが頭に描いた絶対空間説,エーテル説とも,全然異なるものである。むしろ古代ギリシアの哲学者アリストテレスの考えを思わせる説である。 それではこの考えのどこが間違っているのだろう。たとえばAからCへ光のビームを送ることを考えよう。Aから鏡Cを目指したビーム光はC′には行かずにCに行くのだろうか。とんでもない。いったいAからCヘビーム光を発射するというとき,どのようにしてビームを作るのかを考える必要がある。レーザー装置を買って使えばいいのだが,ここでは説明のためレーザー装置の代わりに,AからCの方向に普通の光のビームを送る簡単な装置を考えよう。 すぐに思いつくのは,図2.6のように光源の先に筒をつけたものである。その筒をCの方向に向ける。ただし,筒の内側は黒く塗られていて,反射を抑えてあるとしよう。筒はエーテル系で見て,右のほうに運動しているとする。そうすると筒は時間とともにAl,A2,A3と運動するはずである。光源から出た光がそもそも筒を通過するためには,実線の方向つまりC′に向かう方向に進むはずだ。というよりは,この方向に向かう光のみが筒を抜けられるのである。 エーテル系でCに向かった光は筒の側壁に当たって吸収されてしまう。 つまり,実験室系で鏡Cに狙いを定めた筒から出る光は,筒が動いていようが止まっていようが,鏡に当たるのである。このことは,特殊相対論以前の常識の問題で,19世紀流のエーテル理論だろうが同じことである。19世紀の学者といえど,こんなバカげた間違いは決してしない。 光の進む方向が,光源の観測者に対する運動によって異なってくるのは,光行差と関連した現象である。その具体的な公式などは次章に譲る。 (図2.6は、下図の図-15に対応します。) |
 |
 |
松田氏は、“レーザー装置を買って使えばいいのだが,ここでは説明のためレーザー装置の代わりに,AからCの方向に普通の光のビームを送る簡単な装置を考えよう。”などと書いて、何故レーザー光線で説明されないのでしょうか?
その上、何と無く説得性があるようで可笑しな「図2.6 ビーム発生装置」なるものを持ち出してきたのでしょうか?
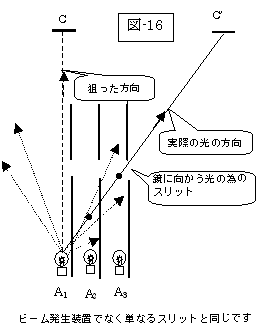
そして、上の右図(図-16)で示しましたように松田氏が期待した「ビーム発生装置」は、四方に発射された光を「A1-C’」の方向にのみに選択する「単なるスリット」と云うか、「目的を限定したスリット」でしかありません。
若しも、この「ビーム発生装置」であると云うなら、「光源の先に筒」の長さに制限は無い筈です。
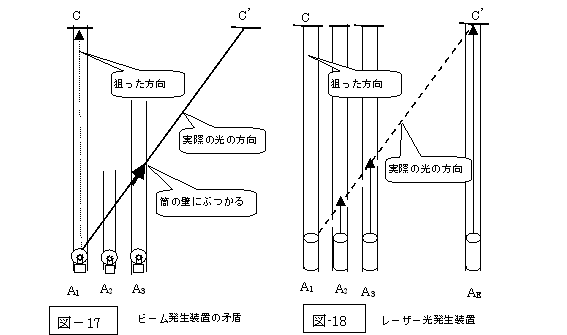
だとしましたら、下の左図(図-17)のA3の位置を注目頂きましょう。
ここでの筒の長さが若干長かったら、光は全く外に出られなくなります。
「光源の先に筒」の長さは、A1の位置に書きました如くに天井までの長さがあっても「ビーム発生装置」ならば、文句は無い筈です。
となると、松田氏の説明では、氏の掲げた図の斜め(実際の光の方向)の光は、本当に外に出られなくなります。(真上に向かった光のみが筒から外に出られるのです。)
更に付け加えますなら、下の右図(図-18)の如くに、光源を白熱電球から、レーザー光に変更しても、「特殊相対性理論」の説明には支障は無いはずです。
ところが、当然この場合も、松田氏の説明は全く無意味となってしまうのです。
と申しますよりも、下の右図(図-18)にて「特殊相対性理論」の説明がなされるべきと存じます。
 |
そして、上記抜粋文の最後には、“光の進む方向が,光源の観測者に対する運動によって異なってくるのは,光行差と関連した現象である。その具体的な公式などは次章に譲る。”と書かれながら、この件に関しての「光行差」による松田氏の説明は有りませんでした。
そこで自分で考えるしかないと思いました。
先ず考えられるのは、走ってくる電車の中に、上の右図のような「レーザー発生源から天井の鏡まで届いている筒」が立っていたら、電車の外にいる人はその筒がどのように見えるのだろうか?
若しかしたら、上図の「実際の光の方向」(A1C’の方向)に「A1Cの筒」が傾いて見えるのではないだろうかと思いました。
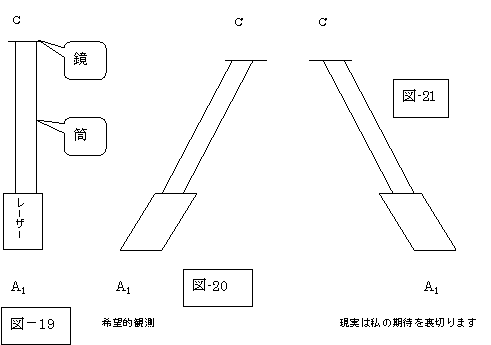
ところが、『時空図で理解する相対性理論』(和田純夫著:1998.12.10:ナツメ社発行)の118頁には、以下の如くに書かれて降りました。
|
縦向きの棒が目の前を通り過ぎるとき、人間の目にはどのように見えるか考えてみよう。縦向きとは、棒の進行方向と棒の向きとが垂直な場合のことである。右の図のような場合、棒の中央ではなく、下端が目の一番近くを通過する。上端は少し離れた所を通過する。 問題なのは、棒の両端からくる光が目に到達するまでの時間差である。下端は目の一番近くを通ったとしても、上端はそれよりも棒の長さだけ遠方を通っている。そして、上端からの光が観測者の目に届くまでに、棒も動いている(これは相対性理論とは関係ない)。 つまり、目に同時に到達した棒の両端からの光は、上端からの光の方が、過去の位置を示している。つまり、実際は棒は正確に縦向きでも、上側のほうが遅れているように見える。つまり、棒は傾いて見えるのだ。 |
確かに、問題の筒は傾いて見えるようですが、傾き方が上図の「実際の光の方向」(A1C’の方向)、と逆に、下図の右端の図(図-21)の如くになってしまうのです。
 |
そこで今度は自分で考えることにしました。
ここまで二冊の「相対性理論」の本を読んできて悟りましたことは、
1.)今現在、“何が起こったか?”を認識するには、光の速さでしか認識できない。
2.)更に、「一瞬にして」というのは存在しない。私達が今まで、「一瞬にして起きた」と認識していた“現象”には、必ず、限りなく短い時間であるが「或る有限の時間に起きた」と解釈しなくてはならない。
3.)従って、光といえども私達が今まで“一瞬きらめいた”と言う表現は不適格で、“限りなく短い時間であるが「或る有限の時間の間」きらめいた”と表現しなくてはならないでしょう。(光が光子であっても、その進行方向を定めるには、やはり「或る有限の時間」が必要なのです。)
この3点を頭に入れて、
電車の中の人が、
“レーザー光線を電車の天井(真上)に向けて発射した”と言う現象は、
“レーザー光線を「一瞬」電車の天井(真上)に向けて発射した”と云う事でなく
“レーザー光線を「限りなく短い時間であるが或る有限の時間」電車の天井(真上)に向けて発射した”
と云う事なのです。
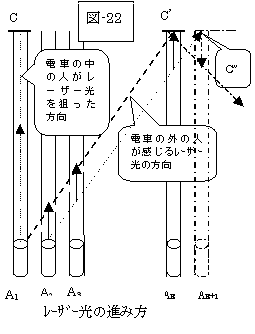
ですから、電車の中の人が、“レーザー光線を「限りなく短い時間であるが或る有限の時間」電車の天井(真上)に向けて発射した”場合は、(前掲の図-13のような事態は考慮の対象外で、)図−17は、下図(図-22)の如くに書き換えて考えられるでしょう。
(尚、下図において、「限りなく短い時間であるが或る有限の時間」において、電車がA1からA2に移行し、矢印はその時間の間で電車の中の人が認識するであろうレーザー光)
 |
この図にて、説明します。
但し、「限りなく短い時間であるが或る有限の時間」と言うのは、時間は短くても表現が長いので、以降は、この時間を「Δ時間」と表記いたします。
(それからもう一つ付け加えさせて下さい。
レーザー光ですから、光源の先の筒は不要ですが、光源と鏡の関係を明確に位置付ける為、それから、レーザー光の進行状況が、どの地点からも目視出来るように、この筒の中にレーザーの進行を邪魔しない様に煙を蓄える目的として残していると解釈して下さい。)
電車の中の人がA1からCに向かって電車の天井(真上)に向けて「Δ時間」レーザー光を発射したとしますと、その「Δ時間」後には、電車はA2に来ており、レーザー光の先端はそこの矢印の先端に来ています。
そして、次の「Δ時間」後には、電車はA3に来ており、レーザー光の先端は、ここでもA2の場合と同じように、そこの矢印の先端(斜めの点線上)に来ています。
この事態を何度も繰り返して、最終的には、光源がAEまで移行した時点では、右図の如くにレーザー光の先端は電車の真上の鏡に到達するでしょう。
この結果、電車の外の人は、レーザー光の先端は、矢印の先端を結んだ線上(図-22の点線上)を進んで行くと認識するでしょう。
では、矢印の後端はと申しますと、A1で矢印の先端が発生したのと全く同様に、A2の時点(位置)で矢印の後端に相当するレーザー光が発生したで発生し、以降矢印の先端の場合と同様にA3 A……と進み、AE+1迄に、光源が来た時に、矢印の後端に相当するレーザー光は、電車の天井の鏡に到達するでしょう、そして、その時には矢印の先端に相当するレーザー光は図の一点斜線の矢印の先端となって、図の斜めの一点斜線上に反射波となっているでしょう。
更に付け加えますと、今までの説明では、レーザー光は「Δ時間」だけの発射で連続発射ではありませんでした。
では、レーザー光を連続的に発射したらどうなるのでしょう。
それは、今説明した、レーザー光の先端と後端の話を次から次へと続けて行くのと、同等(等価)なのです。
この点を、次図(図-23)で(図-11)における光源の移行位置を、AE以降を用いて説明しましょう。
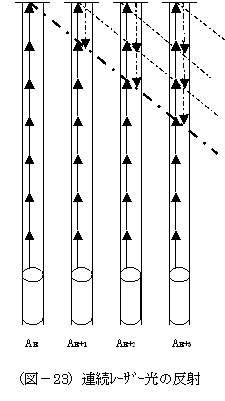 |
光源から「Δ時間」単位に連続的に、レーザー発射されるならば、右図(図-23)にご覧頂きますように、連続的に発射されるレーザー光を矢印毎の単位に分割して、(図-11)同様に「Δ時間」毎に、考慮しても差し支えないでしょう。
そして、レーザー光源の先端が鏡に届いた時点、地点のA以降は、光源がどの位置に移行しましょうが、鏡からの反射光は、分割単位毎の量(矢印の本数)を、1本→2本→3本→……と増大して行きます。
その結果、電車の外の人は、光の軌跡を右図(図-23)の太い斜めな一点斜線の如くに観察するでしょう。
但し、蛇足ながら付け加えますと、レーザー発生装置の筒などの形状は、電車の外の人には、前述の(図-21)の様に、斜めに見えるでしょう。
そして、下図(図24)の様に、
電車が遠ざかるに従って、(電車の外の人に対しての)電車の天井の鏡と、レーザー光源との光路差が減少するので、斜めの角度は徐々に解消されて行くでしょう。
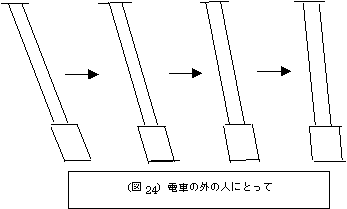 |
ここまで、論を進めてきましても、何故、電車の中の人だけに、光が真上に向かう様に見えて、電車の外の人には、斜めに見えてしまうのでしょう。
それは、光源が電車の中にあるからです。
そこで、次には、光源(レーザー光源)が、電車の外にある場合を考察してみましょう。
通過する電車の真下(床の高さに相当する高さ)にレーザー光源を置き、電車の天井の高さに相当する位置に鏡をセットして、電車の通過を待ち構えます。
(勿論、電車の真下からでなくても、電車のレールに直行する位置関係に、レーザー光源と鏡をセットしても良いのです。更に、その時の光源と鏡の高さは、電車の中で観察する人の目の高さに調整しておくと良いでしょう。それから、光が電車の筐体に遮られない為には、電車は透明である方が良いでしょう。
この場合の状況を、次図(図25)に示します。)
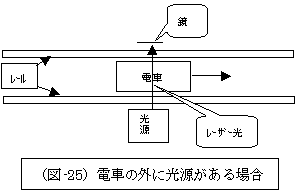 |
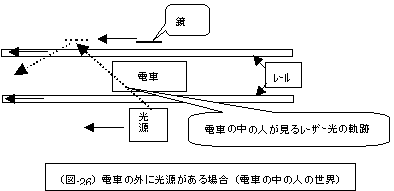 |
今度は、電車の外にいる人は、光源と常に同じ位置関係にいますから、レーザー光は自分の位置から真っ直ぐに発射され、鏡に当たって、真っ直ぐに帰ってくるのを観察出来るでしょう。
ところが、電車の中の人は(先ほどの場合で電車の外の人が観察したのとは逆に)光源(鏡もレールも)が電車の進行方向と逆に遠ざかって行くのを観察するでしょう。
この結果、(図22)(図23)における電車の外の人と電車の中の人とは、立場を全く逆転し、且つ、観察される現象は左右対称的な現象として観察され、電車の中の人は、上図(図26)の様にレーザー光が斜め後ろに進み鏡に反射して行くのを見るでしょう。、
以上の様に、光源が電車の中にあるか、外にあるかで観察される状況が全く逆転するのです。
即ち、自分(A)と同じ速度で動いている物(B)は、自分(A)が止まっていると認識するなら、その物(B)も止まっているのです。(今回の場合は、光源はB)
3.)双子のパラドックス
ここまで長々と自分なりに論を進めて、前掲の『時空図で理解する相対性理論』(和田純夫著)の67頁〜73頁での、走っている電車の中の鏡による光の反射の事例による、「時間」を観測する人が、「電車の中か外に居るかの相違」で、「観測される時間にズレが生じる」事への説明がすっきりしてきました。
しかしながら、同書の94〜101頁で展開される『アインシュタインの相対性理論』の有名なパラドックスである「双子のパラドックス」への説明は、全く納得が出来ないのです。
その部分を抜粋してみます。
(お断り:以下の図に於いて、ロケットの図が飛行機になったり、矢印になったりと、私の図が不備な点はお許し下さい)
|
双子のパラドックス 〜何が不思議なのか〜 相対性理論では、「時間が遅れる」とか「長さが縮む」とか、一見すると奇妙なことが起こる。しかしあくまでも、一見したときに奇妙なだけであって、よく考えるとつじつまがあっているという、実にうまくできた理論である。
しかし世の中には、何とかして相対性理論の欠陥を見つけだそうとする人がたくさんいて、相対性理論を信じるとおかしな結論になってしまう現象があると主張する。
そのような現象をパラドックスと呼ぶ。しかし相対性理論がつじつまのあった理論である限り、その現象がいかにおかしく見えたとしても、よく考えれば理屈にあっていなければならない。
この章では有名なパラドックスをいくつか取り上げて紹介する。
それらが相対性理論によって、いかにうまく説明されるかを解説していこう。
双子の兄が、超高速の宇宙船に乗って宇宙旅行に出掛ける。(自分を基準にした時間で)10年たったときに反転し、20年後に地球に戻る。兄は20才歳を取ってしまったが、弟は何才歳を取っているだろうか。
まず単純に考えよう。動いていると、すべての現象はゆっくりと進行する。宇宙船は動いて、時計は遅れるのだから、兄のほうが若くなる。
しかし挙げ足を取りたい人は、次のように言うだろう。「運動とは相対的なものだ。兄を基準にして見れば、地上の弟が動いている。だから、若いのは弟のほうだ」と。
〜兄と弟の違い〜
基準によって結論が違ってしまう。では、相対性理論が間違っているのだろうか。
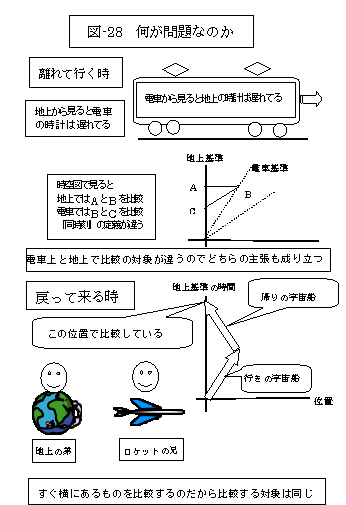
このような話は前にもしたではないか、と言う人もいるかもしれない。前章では、互いに動いている人にとっては、互いに相手の時計が遅れて見えると言った。そして、時空図で見ると比較の対象が違うので、矛盾ではないと説明した。「場所が離れていると同時刻の定義が基準によって異なる」ということが、ポイントだった。 しかし今回はそうはいかない。兄は地球に戻ってくる。弟のすぐ横に立ってお互いの歳を見比べるのだから、比較の相手が違うなどということはありえない。
結論は一つだ。若いのは兄のほうである。つまり、弟を基準にしたときの答えが正しい。
では、なぜ兄を基準にして考えてはいけないのか。それは、兄が途中で方向転換しているからである。
もともと相対性理論での運動の相対性とは、相手に対して(方向も含めて)同じ速度で動いているときには、どちらを基準にとっても構わないということだった。途中で方向を変えてしまっては、相対性理論で認められる「一つの基準」とは言えなくなるので、兄を基準にした議論は間違っている、というのが結論だ。
しかし次のように考えたらどうだろうか。(宇宙船が等速として)行きだけ考えれば、兄
を基準にしてもいい。また帰りだけを考えれば、やはり兄を基準に考えてもいい。
ではその二つを組み合わせて、兄を基準としたときの答えが成り立つとしてはいけないだろうか。
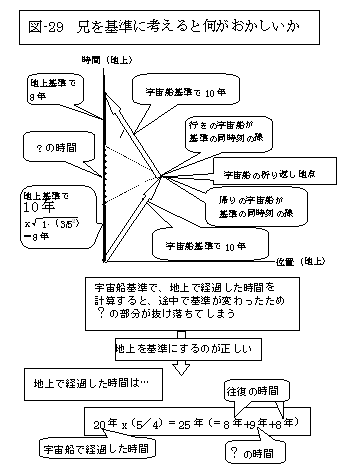
〜兄を基準にして考えると〜 相対性理論で一見すると矛盾した結論が導かれたら、時空図を描いてみるといい。 どこを勘違いしているのかがよくわかる。 光速度の3/5の速度で飛び出した双子の兄が、自分の時計で10年たったときに、また、同じ速度で地球に戻ったとしよう。右ページではそれを、地球を基準にした時空図に描いた。 まず、行きの宇宙船を基準に考えてみよう。宇宙船から見れば、地球がその速度で遠ざかっている。したがって宇宙船の時計で10年たったとき、地上の時計は8年しかたっていないはずだ。 しかしこれはあくまでも、宇宙船を基準にした同時刻での比較だ。 そしてその同時刻の線は、右ページの時空図では、右上がりの線になる。つまり、地球の時計での8年の目盛りは、宇宙船の時計の10年の目盛りの左下にある。 また、帰りの宇宙船は方向転換して、左向きに動いている。したがって、帰りの宇宙船を基準にした同時刻の線は左上がりになる。 つまり、反転したときと同時刻での地上の時計の目盛りは、宇宙船の時計の10年の目盛りの、斜め上にある。そして、それから兄が戻るまで、地上の時計は、8年しか進まない。 つまり、時空上での比較する部分を間違わなければ、宇宙船の行き、帰り「それぞれ」で、兄から見て地上の時計は確かにゆっくりと進む。 しかし行きと帰りの8年を加えても、地上で経過した時間全体を表していないことは、図から明らかだ。基準が途中で変わってしまうからだ。あくまでも、地上の弟を基準にした考え方が正しい。
|
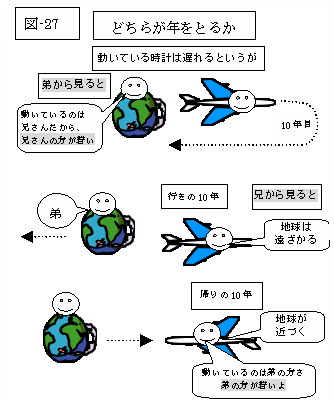 |
 |
|
 |
この和田氏の見解は前出の松田氏もほぼ同じ見解です。
しかし若干異なる見解の部分があります。
そこで、松田氏の著作『なっとくする相対性理論』の78頁の部分を抜粋してみます。
|
兄と弟は完全に対林的な立場にいるのではないのだ。問題は,兄が目的の星でロケットの方向転換をするところにある。方向転換をするためには,ロケットを噴射してブレーキをかけて減速し,そして再び地球のほうに向けて加速しなければならない。減速も加速の一種であるから,ロケットは方向転換のときに加速度運動をするということができる。するとこのときに,みかけの力が発生する。ところが弟には,兄の方向転換のときに,このようなみかけの力は発生していない。 だから二人の立場は対称的ではないのである。やはり弟と全宇宙が静止していて,兄はそれに対して運動していると考えるべきなのである。 |
ここで松田氏は、“方向転換をするためには,ロケットを噴射してブレーキをかけて減速し,そして再び地球のほうに向けて加速しなければならない。”と書かれていますが、だったら、ロケットの地球からの「発射時」にも、地球への「停止時」にも「加速」「減速」による「みかけの力」が働いている筈です。
松田氏はこの「みかけの力」をどう考えているのでしょうか?
この「みかけの力」は、ロケットの時間に影響しないのですか?
影響しないのなら(影響するとしても)、ロケットは、下図(図-30)の如くに対照的な力を受けるので、「みかけの力」の影響はキャンセルされるのではないでしょうか?
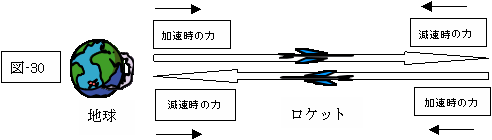 |
(ロケットの「加速時の力」と「減速時の力」を等しくするなら、ロケットは、「行き」(そして、「帰り」)の間に、この二つの力の影響はキャンセルされるでしょうし、又、この二つの力が等しくないとしても、「加速時の力」も「減速時の力」も、各々、「行き」と「帰り」の間にキャンセルされるでしょう。)
ですから、ここでは松田氏の「みかけの力」は除外して、和田氏の見解への考察を進めます。
先に、和田氏の解説を逐一掲載しましたが、この中で、“まず単純に考えよう。動いていると、すべての現象はゆっくりと進行する。宇宙船は動いて、時計は遅れるのだから、兄のほうが若くなる。”と述べ、且つ、 “しかし挙げ足を取りたい人は、次のように言うだろう。「運動とは相対的なものだ。兄を基準にして見れば、地上の弟が動いている。だから、若いのは弟のほうだ」”と言い、“結論は一つだ。若いのは兄のほうである。つまり、弟を基準にしたときの答えが正しい。”と「双子のパラドックス」を和田氏は地球基準でのみ解釈すべきと書いています。
前述の松田氏も、又、『宮沢賢治・時空の旅人』(竹内薫/原田章夫共著:1996.3.18:日本経済新聞社発行)の竹内氏も、同様な見解を披露していますし、多分『アインシュタインの相対性理論』を紹介するどの本にいて於いては、この様に解説されているのでしょう。
でも、私にはとっても可笑しく感じます。
「地球に居る人は、地球上の時間も、ロケット上の時間も認知することが出来る」しかし、「ロケット上の人は、ロケット上の時間はともかく、地球上の時間を認知できない」なんて、片手落ちの事態が相対論の世界で許されるのでしょうか?
和田氏は、“相対性理論での運動の相対性とは、相手に対して(方向も含めて)同じ速度で動いているときには、どちらを基準にとっても構わないということだった。途中で方向を変えてしまっては、相対性理論で認められる「一つの基準」とは言えなくなるので、兄を基準にした議論は間違っている、というのが結論だ。”と述べます。
ところが、 “しかし次のように考えたらどうだろうか。(宇宙船が等速として)行きだけ考えれば、兄を基準にしてもいい。また帰りだけを考えれば、やはり兄を基準に考えてもいい。ではその二つを組み合わせて、兄を基準としたときの答えが成り立つとしてはいけないだろうか。”と 折角、論を進め直しておきながら、「宇宙船の折り返し時点で、?の時間が発生してしまう。」と決め付け、ロケット基準での観察を否定してしまいます。
竹内氏は、『宮沢賢治・時空の旅人』の164頁から(下記に抜粋)は、和田氏の「?の時間」を「失われた時間」と呼び、和田氏同様な結論を導き出して居るのです。
|
本来、相対論では、みんな平等で、運動も相対的なはずです。地球が止まっていると考えれば、動いているロケットの時計が遅れるのは当たり前ですが、逆に、ロケットが止まっていると考えてもいいはずです。 ロケットが止まっていると考えれば、動いている地球の時計が遅れるように見えるはずなのです。 「時計が遅れる」というのは、いつも「動いている相手の時計が遅れて見える」という主観的なことがらのはずでした。ところが、今起こっていることは、そのような主観的で相対的な現象ではありません。誰から見ても、客観的に、ロケットの時計が遅れてしまったのです! これが「双子のバラドックス」のパラドックスたるゆえんです。 みなさんは、もうお気づきでしょうか? 今までは、斜軸が同時に二つ出てくることがありませんでした。でも、今度は、二つの斜軸が同時に時空図に重なっているのです。そして、この二つの斜交軸がパラドックス解決の鍵を握っているのです。 座標軸の原点は、どこでもかまいませんから、図では、二つの斜めの座標軸を折り返し点に集めてあります。さて、空間軸X’とX’’は、それぞれ行きと帰りの「同時刻線」です。折り返し直前の同時刻線を左に伸ばして地球の時間軸tと出会った点を灰色の○印であらわし、折り返し直後の同時刻線を左に伸ばして地球の時間軸tと出会った点を黒の○印であらわすと、奇妙なことが判明します。 折り返しの直前と直後とでは、ロケットの乗組員にとっては一瞬でしかありません。 しかし、直前と直後の地球での同時刻の間は、二つの○印の間(図-29の点線「?の時間」)の分、つまり一年以上もあるのです。 これはつまり、ロケットが折り返し点を回る一瞬が、地球では一年以上もかかったように見えることを示しています。逆にロケットの乗組員からすると、自分達は一瞬にして折り返したのに、地球ではいっきに一年以上(和田氏の例では、9年に相当)も時間が進んでしまったことになります。 これは、結局、行きと帰りとで座標軸が変わったために、「失われた時間」が出てきてしまったのです。 ポイントその1……方向を変えると速度が逆になって座標軸が変わるために「失われた時間」が出てきてしまう ポイントその2……座標軸が違うと「同時」の概念が違うために双子のパラドックスは生じる (網掛け下線処理、そして、()内の補足は私が施しました) |
可笑しいではありませんか、“折り返しの直前と直後とでは、ロケットの乗組員にとっては一瞬でしかありません。”と述べながら、その一瞬の間に“地球ではいっきに一年以上(和田氏の例では、9年に相当)も時間が進んでしまったことになります”と論じているのです。
こんな法則がどこにあるのでしょうか?
そして、“方向を変えると速度が逆になって座標軸が変わるために「失われた時間」が出てきてしまう”等と、訳の分からないこじ付けをなさっています。
素直に、「?の時間」やら「失われた時間」等持ち出さず、その時間を無視すれば済む事ではありませんか!
“方向を変えると速度が逆になって座標軸が変わるために「失われた時間」が出てきてしまう”と云わずに、「座標軸別にロケットと地球の時間の違いを観測し、それを合算する」事にすれば良いではありませんか?
即ち、「?の時間」「失われた時間」を無視すれば良いのではありませんか?
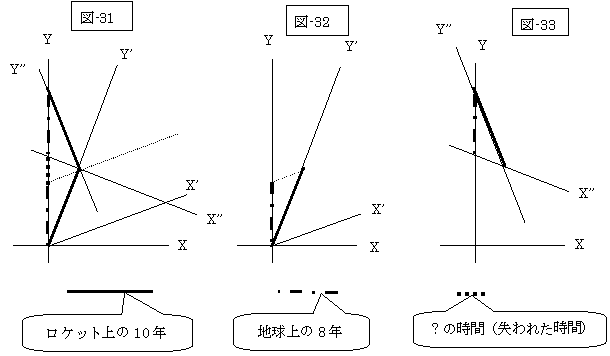 |
上図の図-31の実線(━━)ようにロケットの行き帰りを表さずとも、行きを図-32、帰りを図-33と分割して書いても良いのではないですか?
更に行きと帰りを同一人物でなく、帰りを別の人にバトンタッチ(時計を手渡し)しても良いのではないでしょうか?
(もっと別の考え方をすれば、図-32で折り返し地点まできたロケットが、図-33の折り返し地点に於いて、Y’’のよりマイナス方向からやってきた別のロケットに時計をバトンタッチすると考えたら、和田氏、竹内氏らが問題とするロケットの方向転換という事態がなくなるでしょう。)
そして、やはりこの場合も『アインシュタインの特殊相対性理論』通りに、ロケットを主体にして地球の時間を見れば、(和田氏の例で云うなら)「ロケットでの20年間は、地球上の16年間しか経っていず、地球を主体にした場合と全く逆の結果になる。」との結論のほうが素直ではないでしょうか?
 |
上図の(図-34)の如くに、地球をはさんで等距離にあるロケット甲、乙へ、光で同時に合図を送り、この合図の光信号を受けたと同時に、各ロケットは地球に対して、等速(v)で地球に向かって出発します。
(念の為に、各ロケットは信号を受け、かつ、スタートすると同時に、地球へその旨の光の合図を送り、地球では、各ロケットからのその信号が同時に届いたことを確認します。)
そして、ロケット甲、乙が地球で出会ったとします。
このような状況では、ロケット甲、乙は全く対等です。
ここで、ロケットの地球に対しての速度を、光速の3/5倍(3c/5)として考えますと、ロケット甲,から見たロケット乙の速度は、光速の6/5(=3/5+3/5)倍とはならず、
『なっとくする相対性理論』(松田卓也、二間瀬敏史共著)の83頁を参照します。
|
S系に対して,x軸の正の方向に速度vで運動しているS′系を考える。 そのS′系に対して速度uで運動している粒子を考える。…… また,粒子の速度をS系で測るとwになるとする。すると, w==(u+v)/(1+uv/c2) (c=光速度) となる。これが特殊相対論における「速度の加法法則」である。 とあります。 |
以降、地球の属する系を地球系と呼び、ロケット甲が属する系をロケット甲系と呼びます。
そして、S系(ロケット乙系)に対して,x軸の正の方向に速度v(=3c/5)で運動しているS′系(地球系)を考えるとして、S系をロケット乙系、S’系を地球系と考えます。
更に、S′(地球)系に対してロケット甲が速度u(=3c/5)で運動していると考えます。
このように考えますと、ロケット乙に対するロケット甲の速度(w)は、
w=((3/5)+(3/5))c/(1+((3/5)c×(3/5)c)/c2)=30c/34
と考えられます。
そこで、新たにS系(ロケット乙系)に対して,x軸の正の方向に速度w(=30c/34)で運動しているS’’系(ロケット甲系)を考える事が可能となります。
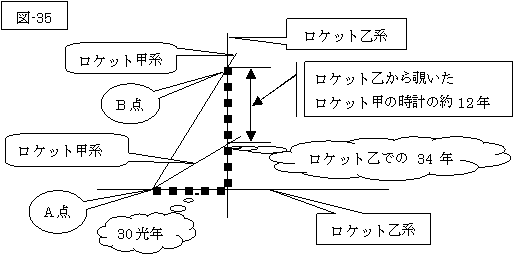
ここで、各ロケット間の距離を、30光年と仮定してみますと、静止した系のロケット乙系と、運動する系のロケット甲系とで、次のような時空図を書く事が可能でしょう。
そして、動いているものの時計は遅れるとの事から、ロケット乙の時計が34年経過する間に、ロケット乙から覗いたロケット甲の時計は、約12年(=34×√(1-(30/34)2)を経過しただけとなるのでしょう。
 |
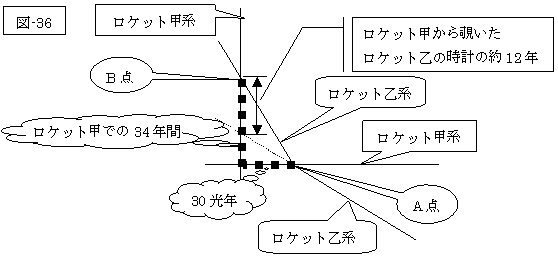
次には、ロケット甲を基準にして考えてみましょう。
下図の如くに、時空の関係が少し変わるだけで、時間の関係は、ロケットの甲と乙の関係が逆転するだけの変化が観察されるでしょう。
 |
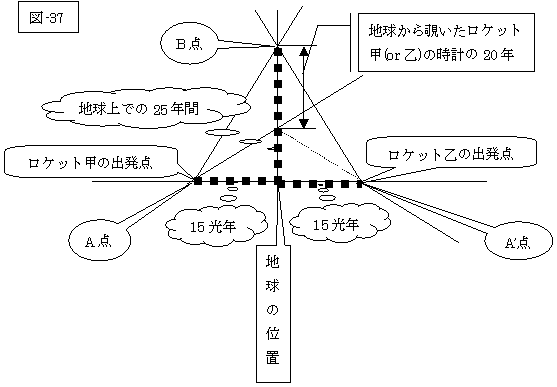
更に、地球を中心に考えてみましょう。
地球から見たロケット甲(or乙)の速度は、3c/5ですから、ロケットは25年で地球に到達し、そのとき地球からロケットの時計を覗きますと、
ロケットの時計は、25×(1+(3/5)2)-1/2=20年と遅れた時間を観察するでしょう。
 |
以上のように、ロケットB、ロケット甲、そして又、地球を基準にして、動いている相手の時計を覗けば皆それらの時計は遅れて見えるわけです。
それにしましても、時間を覗く基準が、ロケット甲、ロケット乙、地球と変わる度に、相手の時間が変わってしまうのは、なんと言っても、基準の取り方がおかしいのであって、“やはり基準は、しっかりした基準を設けるべきであって、地球以外に設定してはいけないのだ!”と、和田、松田、竹内の物理学の先生方はおっしゃるかも知れません。
それでは、次図(図-38)のように地球の変わりに、第三のロケット丙を導入したらどうなるのでしょうか?
即ち、次図の如くに、三つのロケットは等速で同一方向に進行しているなら、この三つのロケットは互いに静止していると見なす事が可能でしょう。
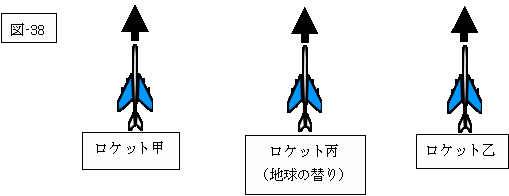 |
そして、地球の替りのロケット丙からの信号を受けた後に、次図(図-39)のようにロケット甲乙が、ロケット丙の方向への速度を加え点線の矢印の方向、速度で進行を開始するなら、この状態は(図-34)と全く同じ状況と認識して差し支えないでしょう。
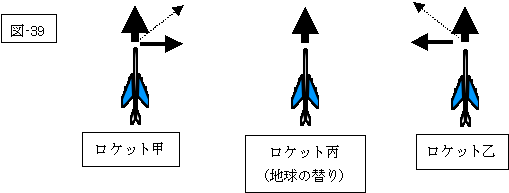 |
でも念の為に、敢えて、(図-40)を付け加えさせて頂きましょう。
三つのロケットの状態を相対的に比較する際には、三つのロケットの移行状態での速度の内、等速分を、三つのロケットの速度から除外しても、何ら問題はないでしょう。
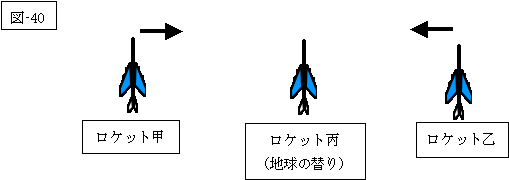 |
そこで、(図-39)から、本紙面の上方向の矢印(それに伴う、斜めの点線)を割愛した
(図-40)を考慮することには問題はないでしょう。
そして、又、この(図-40)は、(図-34)と全く等価と見なせるでしょう。
そして、くどいようですが再度付加えさせて頂きますが、『特殊相対性理論の世界』に於いては、『双子のパラドックス』は、経過時間だけを考えれば、“地球に残った双子の弟を基準にして見れば、宇宙船に乗って戻ってきた双子の兄は、自分より、経過時間は少なく見え、逆に、宇宙船で旅をして来た双子の兄を基準にして、弟を観察すれば、弟の方が経過時間は少なく見える。”と言う『パラドックス』の侭で存在して何ら矛盾はないのです。
そして、この“観察する基準によって、観察される時計は変化する。”と言う新たな認識こそが、『特殊相対性理論の世界』に於いて重要な点なのだと思います。
ここまでお読み頂ければ、松田氏、和田氏、竹内氏らの物理学者達が、双子のパラドックスに対して誤解されている事がお判り頂けたと思うのですが、松田氏、和田氏は彼らの誤解を正当化すべく次の様な論を張っているのです。
先程の和田氏の著書の抜粋に引き続き、同著の100頁から抜粋(説明の図は、(図-41)として掲げます)します。
|
〜手紙をやり取りすると〜 弟のほうが余分に歳を取ることはわかったが、そのずれはいつ起こるのだろうか。宇宙船 が反転することが違いが出る原因だからといって、兄が反転する瞬間に弟が突然、何年問か老けるのだなどと考えてはいけない。 位置が離れている時の兄弟の歳の差は基準の取り方によって変わるので、それを指定せずにいつずれが出るかを考えても、答えが出るはずがない。 そこで、より現実的な質問をしてみよう。兄弟は(それぞれのカレンダーで)定期的に、手紙を電波信号で送り合ったとする。相手はそれを、どのような間隔で受け取るだろうか。 考え方は前に説明した。信号の伝達時間が変わることを忘れてしまえば、遠ざかっているときは常に、相手の時間の進行が遅れているように見える。また近づきつつあるときは、相手の時間の進行は早まっているように見える(76/ヾ−ジ参照)。 つまり兄は、行きは(遠ざかっている)弟の手紙を滅多に受け取らない。つまり、弟がゆっくり歳を取っているように感じる。しかし帰りは、突然、(近づいている)弟からの手紙が頻繁になる。つまり、弟が急に早く歳を取っているように感じる。 弟も同様である。あるときから以降は、頗繁に兄の手紙を受け取ることになる。つまりそれ以降、兄が急に歳を取り出したように感じる。しかし図からわかるように、弟にとっては、手紙を頻繁に受け取る期間のほうが、それ以前の期間よりもかなり短い。兄のほうが歳を取らない理由も、このことからも想像できる。 |
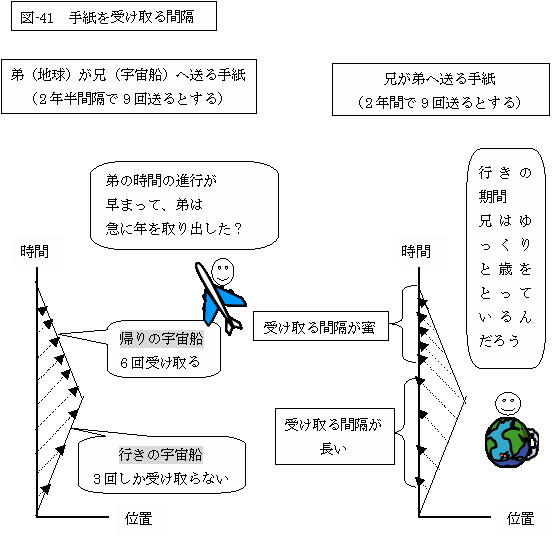 |
ここでの和田氏(松田氏もほぼ同様)の論旨も、可笑しくはありませんか?
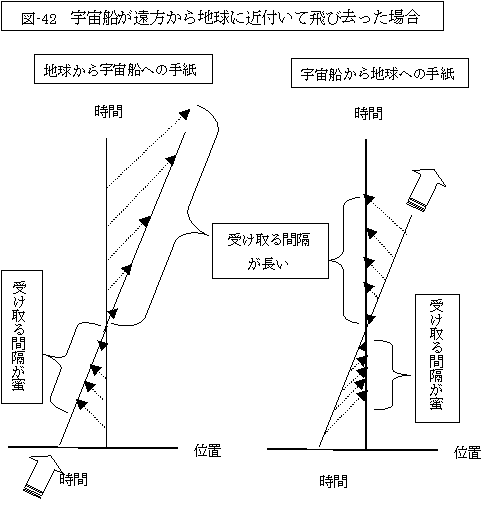
上記の和田氏の地球と宇宙船の位置関係に於いて、宇宙船が当初地球でなく、10年の飛行距離分地球から離れている状態から、地球へ向かって飛行を続け、そして其の侭飛行し続けた場合の時空図を考えてみたら如何でしょうか?
又、次図からも(常識的にも)明らかなように、地球基準であれ、宇宙船基準であれ、宇宙船が地球に近付いてくる場合には、手紙を受け取る間隔が蜜で、地球から離れてゆく場合には、手紙を受け取る間隔が長くなります。
ところが、この場合では、宇宙船は方向転換も何もしていないのです。地球との相対的速度は常に一定なのです。
地球と宇宙船との時間的なズレは常に一定のはずなのです。
即ち、宇宙船と地球との時間的な関係は、「ローレンツの変換」の関係しか存在しないはずです。
なのに、和田氏(又、松田氏も)この場合でも、「宇宙船が地球に近付いてくる間は、時間の進行が早まって、宇宙船が遠ざかり始めると時間の進行が遅くなる。」とおっしゃるのでしょうか?
更に、ここに私が掲げた例での時間的な関係は、和田氏の例(図-41)での宇宙船が地球から離れて行き、又近付いてくる場合と全く同じなのです。
従って、和田氏の例に於いても、「宇宙船が地球から遠ざかる場合には手紙を受け取る間隔が長くなり、宇宙船が地球に近付く場合には手紙を受け取る間隔が密になる。」と言う現象から、「宇宙船が地球に近付いてくる間は、時間の進行が早まって、宇宙船が遠ざかり始めると時間の進行が遅くなる。」と考えてはとんでもない事になってしまうのです。
即ち、先の和田氏の解説は、全くの間違いと言って良いのではないでしょうか?
 |
更に、又、物理学者は色々のパラドックスを紹介して下さいますが、そのパラドックスに対する物理学者の解釈に、双子のパラドックス同様に私は疑問を抱くのです。
4.)紐で結んだ2台のロケットのパラドックス
その一つとして、前述の竹内氏の著書の171頁に紹介されている、「双子のロケット」に関しての竹内氏の解釈を掲載いたしましょう。
|
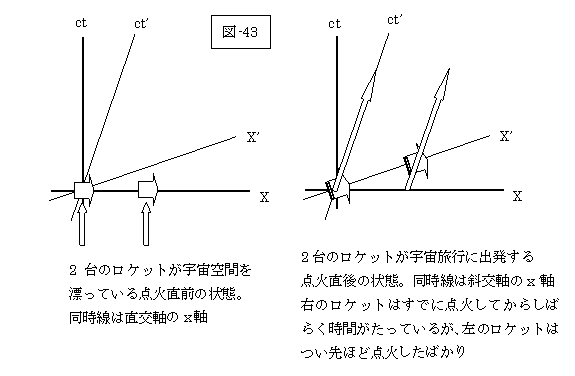
双子のロケット これは超難問です。量子力学の基礎理論でとても有名なJ・S・ベルが提起した問題で、もともとは、 二台のロケットが細いひもでつながれており、はじめ地球に対して静止状態にある。この二台のロケットが同時に点火して徐々に同じ加速度で加速していくと、ひもはどうなるだろうか。ただし、加速は弱くほとんど無視できるくらい小さいため、加速度によってひもが切れることはないものとする。 という形の問題でしたが、ここでは、問題の本質を変えずに簡単化してみます。 二台のロケットが細いひもでつながれており、はじめ、互いに静止状態にある。この二台のロケットが同時に点火して、すぐに巡航速度に達したとすると、ひもはどうなるだろうか。 つまり、加速を無視して、ロケットを点火すると、一瞬にして静止状態から、ある決まった速度になる、と考えるのです。実は、前にやった「双子のバラドックス」 のところでも、折り返し点で一瞬にして速度が逆になる、と考えました。本当は、徐々に減速して止まってから逆向きに加速するのですが、この加速部分を無視したのでした。 このように、問題の本質を変えずに加速度を問題から除去することは、本来加速度を扱えない特殊相対論の枠組みで問題を解く場合には必要なのです。 もちろん、正確にやろうとすれば、加速度も扱うことのできる一般相対論の枠組みで解くべきなのですが、最終的な答えはほとんど変わりませんから、一瞬にして速度が変わった、という近似を使うのです。もともと物理学のセンスというのは、いかに近似をうまく行って問題を簡単化するか、というところにあります。 近似…加速度(徐々に速度が変わる)を無視して一瞬にして速度が変わると考える さて、近似の問題はさておいて、この問題は、なぜ難問なのでしょうか。 これは、早い話が「ローレンツ収縮」の棒(モノサン)のかわりにひもとその両端についているロケットをもってきたのです。ですから、「動いている棒は縮んで感じられる」だけであって、「棒に対して止まっている立場からは、別に縮みはしない」以上、ロケットからひもを見ていてもなんの変化もない、と考えられるのです。 答えは、「ひもは切れない」であるように思われます。ところがこれは大間違いで、正解は「ひもは切れてしまう」なのです。 世界の一流の物理学者が集まっていたCERNにおいて、この問題は侃侃諤諤の議論を引き起こしました。ある高名なノーベル賞学者は、「ひもが切れるなどという世迷い事をいう奴は相対論がまったくわかっておらんのじゃ」と怒り心頭に達したそうです。 私も悪戯好きなので、物理学の大学院生を相手にアンケートをとってみたところ、驚くべきことに、「ひもは切れない」という答えが圧倒的でした。つまり、物理学の専門家でもコロっと間違えてしまうほど、この問題は難解なのです。 相対論のパラドックスの多くは、相対論の効果を全部考えないために生じます。逆に言えば、相対論の効果を忘れずにきちんと考慮すれば、問題はすっきりと解くことができるのです。 図A−4(注:今回は私が(図-43)に書き直しました)を見てください。今までに何回も出てきた時空図です。直交軸が止まっている立場(つまり点火前)で、斜交軸が動いている立場(つまり点火後)の世界観です。図から明らかなように、二台のロケットは、同時に点火したつもりでも、点火後は動いていますから、斜交軸で考えないといけないので、「同時」の意味が点火の前後で変わってしまうのです。右のロケットから見ると、自分のロケットが点火してからしばらくたって、ようやく後続のロケットが点火したように見えるのです。左のロケットからすると、自分が点火する前に(約束を破って)前にいるロケットが早めに点火したように見えるわけです。つまり、二台のロケットをつないでいた細いひもはプッツリと切れてしまうわけです。 ポイント…同時の概念が変わってしまうために、ひもは切れる よく、あの人は相対論がわかっている、とか、あの人は相対論がわかっていない、などという喧嘩に近い議論をみかけますが、この「双子のロケット」問題は、相対論の理解度を試す試金石のようなものです。この問題に正しく答えられるならば、特殊相対論の理解は完璧に近い、ということができるでしょう。もちろん、この問題に正しく答えられないからといって、自分は相対論を理解していない、と落胆する必要はありません。なにしろ、ノーベル物理学賞をとった偉い学者も正しく答えられなかったのですから! |
 |
私は、上記の竹内氏の見解に反対いたします。
“「ひもが切れるなどという世迷い事をいう奴は相対論がまったくわかっておらんのじゃ」と怒り心頭に達した”と言われる“ある高名なノーベル賞学者”の見解を指示いたします。
竹内氏が、“同時の概念が変わってしまうために、ひもは切れる”と思われるなら、先に私が示した(図-37)の如くに、2台のロケットの中間点から光による出発の合図を2台のロケットに同時にしたら如何なのですか?
そして、次のような時空図も書く事が可能でしょう。
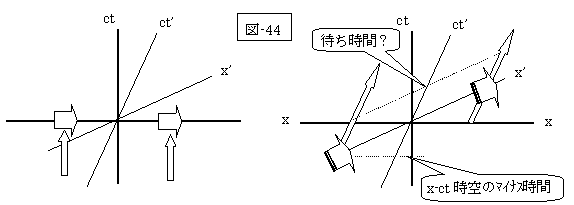 |
竹内氏、(図-44)に対するご見解は?
後続のロケットは、x-ct時空から、x’-ct’時空へ移行するために、x-ct時空のマイナス時間へ移行しなければならないのですか?
それとも、先頭のロケットも後続のロケットも同時に出発の合図を受けていながら(図-44)の斜めの点線とx’-ct’時空のct’軸との交点の「待ち時間?」迄、後続のロケットは待機しているのでしょうか?(そしてその間先頭のロケットは飛び続けている?)
このような不思議な(?)現象が起こってしまうのは、ロケットが静止している時空から、ロケットが動いている時空へ変換する際の物理学者達の誤解なのです。
即ち、図-43の左図(ロケットが停止している座標系)から右図(ロケット進行中の座標系)への移行は単なる「座標の転換操作」であって、この間の時間の概念は無いのです。
(竹内氏も“一瞬”と言っている筈です。)
なのに、竹内氏はじめ物理学者達は、そこにこっそりと時間の概念を導入してしまって居るのです、そして、その事に気が付いていないのです。
ですから、どうしてもこの“一瞬”の言葉の中に時間の概念を導入したいのなら、たとえ“一瞬”と言えどもその“一瞬”の中に時間の経過を忘れてはいけないのです。
ここで、もう一度(図-43)に戻ってみましょう。
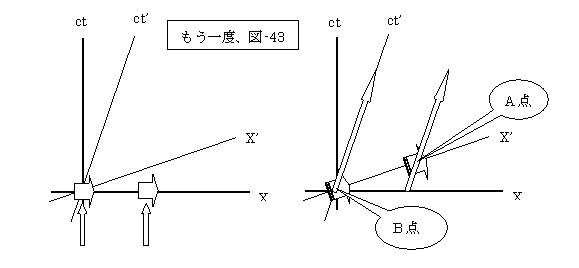 |
ロケットが静止している時空(図-43の左図)から、ロケットが動いている時空(図-43の右図)へ、一気に変換して考えるから、先頭のロケットだけが先に点火して竹内氏の誤解してしまったのでしょう。
竹内氏は、先頭のロケットが上図のA点に移行している間に、後続のロケットがB点に留まり続けていると、考えてしまったことが間違いの第一歩なのです。
(ご自身で書かれた、(図-43)の右図の後続ロケットもB点(原点)に留まり続けてはいるものの、きちんと既に点火済みなのに)
竹内氏は、飽く迄も先頭のロケットも後続のロケットもそしてその間を結ぶ紐も常に同じ時空に存在していると認識し続けるべきなのです。
更に、両ロケットとも同時に点火されているのです。
ですから、この二つのロケットは、次図(図-43(両ロケットと紐を一体化し、一つの矢印として示し、x軸の変化のみを記しました))のように、微少時間を経過しつつ、順次、時空を変更しつつ、最終的な時空へと落ち着くと考えるべきなのです。
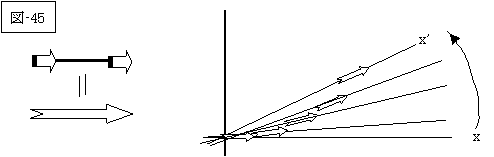 |
そして、このロケットの加速時間をどんどん早くして行けば、(図-43)の時空の変化は、次図(図-44(但し、図を見易くする為に、矢印の大きさを(図-43)より拡大してあります))のように、即ち、(図41の右図)の如くになるでしょう。
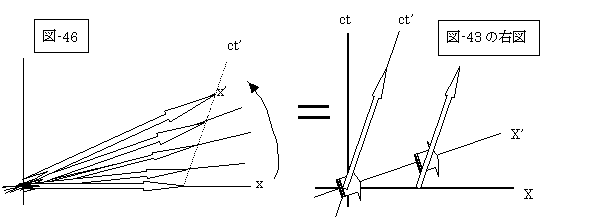 |
このように、両ロケットそしてその間をつなぐ紐は一体となって順次(滑らかに)静止時空(x-ct時空)からロケットの最終的速度の時空(x’-ct’時空)へ移行するのです。
従って、竹内氏の誤った説明の如くに、途中の紐は切れないのです。
ましてや、先頭のロケットが、後続のロケットの点火前に、点火して先に進んでしまうような可笑しな事態は生じないのです。
念を入れて、もう一つ論を進めましょう。
(図-43)に於いて、地球から紐で結ばれた2台のロケットが右方向へ飛び立つ現象と、この2台ロケットと紐をそのままに地球が反対の左の方に飛び立つ(?)現象とは、相対性理論に於いては等価な現象となるでしょう。
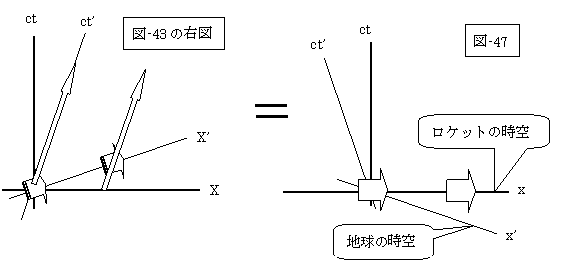 |
上記の時空では、地球だけ動いて、2台のロケットもそれを結ぶ紐も動かなくてすむのですから、その紐は切れるはずはありません。
“「ひもが切れるなどという世迷い事をいう奴は相対論がまったくわかっておらんのじゃ」と怒り心頭に達した”と言われる“ある高名なノーベル賞学者”の見解が正しいのだと私は考える次第なのです。
そして、このような数々のパラドックスに対して、物理学者たちは、“パラドックスではない、矛盾ではない!”と先の地球と宇宙船で旅をした双子の兄弟に対するが如き解釈を披露します。
5.)「ガレージのパラドックス」
その中でも、『ガレージのパラドックス』は、松田氏、和田氏とも取り上げていますが、今回は和田氏の解釈を抜粋いたしましょう。
『時空図で理解する相対性理論』(和田純夫著)の112頁には、
|
〜車をガレージに突入させると〜 ……車をガレージの中に入れたい。しかし残念ながら、ガレージよりも車のほうが長い。 しかし、この車の持ち主は相対性理論を知っていた。動いているものの長さは短くなる。 そこで彼は、超高速で車をガレージに突入させ、車の先端がガレージの奥の壁に到達した瞬間に、横で見ている奥さんに、ガレージの入り口を閉じてもらえばいいと考えた。走っている車は短くなるから、車はガレージの中にうまく入るというのだ。 しかし彼の奥さんは、運動とは相対的なものだということを知っていた。車を基準に考えれば、ガレージが動いている。したがって、車から見るとガレージが縮むので、事態はよけいに悪くなる。車は入り口のシャッターに押しつぶされてしまうから、馬鹿なことはするなと言った。 確かに運動は相対的なものだが、車がシャッターに押しつぶされるかどうかが、見る人の基準によるはずがない。だから、彼と奥さんと、どちらの見方も正しいとは言えない。ではどちらが正しいのだろうか。 ところで普通の人だったら、超高速で車をガレージに突入させたら、ガレージの壁か車か、おそらくはその双方が、壊れてしまうと考えるだろう。しかしここではその心配をする必要はない。幸もガレージも非の打ち所がないもので、蹴っても殴っても傷一つ付かない最高級品だとしよう。では、ガレージに突入した車は、シャッターが下りたときどうなるだろうか。 〜車はガレージに入る〜 ガレージを基準にすると、車は縮んで見える。しかし車を基準にするとガレージが縮んで見える。では、入り口のシャッターを下ろした瞬間には、車はガレージの中に入っているのだろうか。 今までこの本を読んできた皆さんならば、どこにこの問題を解く鍵があるのか、想像できるだろう。 車の先端がガレージの奥に到達した瞬間に、つまりそれと「同時刻」に、入り口のシャッターを下ろす。しかし「同時刻」かどうかは、基準によって異なるということを、何度も言ってきた。横に立っている人にとって同時刻だとしたら、車を運転している人にとっては同時刻ではない。これが、この問題を解く鍵だ。 まず地上を基準にして、この実験を考えてみよう。シャッターを下ろすのは、地上に立っている奥さんである。つまり、車の先端がガレージの奥に到達するのと、入り口のシャッターを下ろすのは、地上を基準にしたときの同時刻である。 そして地上から見ると車は縮んで見えるのだから、車はシャッターに押しつぶされることなく、ガレージの中に入る。ただし、入ってからどうなるかは後で考えよう。 では、車に乗っている人にはどう見えるだろうか。地上基準で同時刻の二つの現象は、車を基準にした時間では、進行方向のものほど早い時間に起きているように見える。つまり、車の先端がガレージの奥に到達して少したってから、入り口が閉まる。実は、この少しの間に車の後部はさらに前に進むので、車はガレージの中に入ってしまうことになるのだ。 〜車は本当に(基準とは無関係に)縮む〜 車を基準にして考えても、車はガレージの中に入る。…… 車は簡単には止まらないので、ガレージの中に入ってしまうというのが、正解である。車の先端が壁に到達したときは、(車基準では)最後部はまだガレージの外にある。しかし先端が到達したという情報が最後部に伝わるまでには、時間がかかる。いかなる情報や信号も、光速度以上では伝わらないというのがポイントである。…… いかに頑丈な車であっても、相対性理論を考えると、かならず縮むのだ。…… |
ここに抜粋しましたように、和田氏は“動いているものの長さは短くなる”と言うことで、“ガレージよりも車のほうが長い”のに、“車はガレ-ジに入る”と解説するのです。
勿論、“地上を基準にして”考えるなら“地上から見ると車は縮んで見えるのだから、車はシャッターに押しつぶされることなく、ガレージの中に入る。”と言う論は取り敢えず成り立つでしょうが、“車を基準にして考えても、車はガレージの中に入る”との見解には呆れてしまいます。
その理由としての“先端が到達したという情報が最後部に伝わるまでには、時間がかかる。いかなる情報や信号も、光速度以上では伝わらないというのがポイントである”と記述されるのですから。
だったら、車の運転席が車の中央にあったらどうなるのですか?
(最後部にあったら?)
和田氏は、「地上基準でも車基準でも何が何でも車をガレージに入れてしまおう。」
そして、“車は本当に(基準とは無関係に)縮む”“相対性理論を考えると、かならず縮むのだ”との、物理学者とは思えないとんでもない間違った結論を導き出そうと詭弁を弄しているように思えます。
本当に、物理学者たる和田氏は「相対性理論」を理解されているのでしょうか?
「相対性理論」に於いても、動いている時空の物体(自動車)は、静止している時空(地上)から見ると、物体(自動車)の大きさは縮んで見えるのですが、あくまでも縮んで見えるだけで、実際(動いている時空に於ける)の寸法は縮んではいないのです。
ですから、和田氏の“車は本当に(基準とは無関係に)縮む”“相対性理論を考えると、かならず縮むのだ”との見解は全くナンセンスなのです。
宇宙には、多くの星々が我々の地球に対して様々な速度で移行しています。
そして、相対理論的に考えるなら、その様々な速度で移行する星々を基準にして我々地球を覗くと、我々地球は(基準とする星々の相対的速度に応じて)様々な速度で動いている事になるでしょう。
そして、その結果我々は基準となる星の速度に従って様々な寸法に縮んでしまうのです。
(光速に近い星を基準にして地球を見れば、我々は無限に小さく縮んでしまうでしょうし、又、別の速度で動く星を基準に選べば、瞬時に別の寸法に変化するのです。このように我々の寸法が不確かでは生きてはいけません。)
もう和田氏の見解の間違いがおわかりいただけたと思います。
和田氏の、“車は本当に(基準とは無関係に)縮む”との見解は、「アインシュタインの相対性理論の世界」ではなく、エーテル説を信奉したローレンツ達の世界です。
ローレンツ達は「動いている物は実際に収縮する」
アインシュタインの世界では、「動いている物は収縮すると観測される」で、実際に収縮するのではないのです。
従って、我々の一般的常識としての「寸法」(「距離」)の概念では、地上基準で見れば、動いている車の寸法は縮んで見えガレージに入ると観察されますが、車基準で見れば逆に地上(ガレージ)が収縮して、車(たとえガレージと同一寸法であっても)はガレージに入れないと観察されるのです。
ところが「アインシュタインの相対性理論の世界」では、「距離」も「時間」も明確な区別が付けられないのです。
従って、「アインシュタインの相対性理論の世界」では、「四次元距離」とか、「固有時間」なる概念の導入がなされているのです。
この件に関しましては、次章に譲ります。
6.)ミュー粒子(ミュー(μ)オン)の寿命
更に続けますと、同じく『時空図で理解する相対性理論』(和田純夫著)の172頁には次の様に書かれています。
|
〜ミユー粒子の寿命〜 (前略) ミユー粒子という素粒子は発生しても、短時間で電子と、ニュートリノと呼ばれる粒子に変化してしまう。発生してから他の粒子に変化するまでを寿命と呼ぶが、人間と同じで寿命にはばらつきがある。しかし平均寿命は決まっていて、ミユー粒子の場合は10万分の1秒程度である。 しかし、ミユー粒子が動いている場合はそうではない。相対性理論によれば、動いている物体では現象はゆっくり進む。したがってミユー粒子が動いていれば、平均寿命も延びるはずだ。実際、ミユー粒子を加速器で光速度の99.94%にまで加速し、平均寿命が予想通りに延びていることが確かめられている。 ミュー粒子が光速度の99.94%で動いたとすると…… v/c=0.9994のとき 1/√(1-(v/c)2)=約29倍 (時間の進み方が遅れるので、ミュー粒子の寿命が約29倍伸びる) |
和田氏は、“相対性理論によれば、動いている物体では現象はゆっくり進む。”と書かれていますが、これでは表現が不適切です。
あく迄も、「相対性理論によれば、動いている物体では現象はゆっくり進むように観察される。」のであって、動いている物体自身が現象がゆっくり進むようには認識しないのです。
なにしろ、我々の属している宇宙空間には、絶対的な基準は無いのですから、動いていると言っても、飽く迄も「相対的な動き」なのです。
先ほどの例と同様に、宇宙には、多くの星々が我々の地球に対して様々な速度で移行しています。
そして、その星々の中で、地球から光速に近い速度で移動する星に注目して、その星から我々の地球を覗いたら、我々の地球は光速度に近い速度で動いている事になるでしょう。
ここで、和田氏の見解に従うなら、光速度に近い速度で動く我々は、無限に近い寿命を得ることになってしまいます。
(なのに、地球に目を向けるとたちまち通常の寿命に戻ってしまうのです。又、別の速度で動く星を見れば又別の寿命になるのです。)
遠くの星々の速度がどう変わろうが、我々の寿命に影響を及ぼさないと同様に、我々から見てミュー粒子の時間が遅れようが、ミュー粒子から見て我々の時間が遅れようが、互いの寿命への影響力は無視出来ましょう。
例えば、ミュー粒子が地球上でなくて、(周囲に何も無い)遠くの宇宙で、加速されたらどうなりますか?ミュー粒子は加速された事をどのように自分で感じるのでしょうか?
(彼方に輝く星を見てでしょうか?だとしたら星々は色々な速度で移行しているのですから(少なくとも、我々の地球を基準として測ると)それらの星々の内でどの星を基準とするかで、ミュー粒子の運動速度は色々に変化しまうでしょう。その結果、ミュー粒子の寿命も色々に変化してしまい訳が判らなくなってしまいます。)
可笑しなことですよね!
ですから、“ミュー粒子の寿命が伸びた”と我々が認識するのは、ただ単に高速で運動するミュー粒子を観測すると、ミュー粒子の時計が遅れて進むのが観測される結果、あたかもミュー粒子の寿命が延長されたように、我々からは観測されるだけであって、決してミュー粒子自体の寿命(ミュー粒子自身が自分の時計で測った寿命)は不変なのです。
もう一点、ここで松田氏の「なっとくする相対性理論」の76頁を抜粋させて頂きます。
|
運動する時計が遅れるということの,一番よい例はミユーオンである。 主として陽子からなる宇宙線が,宇宙から地球にやってくる。地球の大気のてっペんで陽子が空気の分子と衝突して,ミユーオンという素粒子を発生させる。ミユーオンは地表に降ってきて観測されるが,この素粒子は極めて不安定であり,できてすぐに崩壊してしまう。だからたとえ光速度で地上に降り注いでも,途中で崩壊して,地上にまでは到達しないはずである。しかし,現実には到達しているのだ。 その理由は,ミユーオンの速度があまりにも速くて光速度に近いので,地上の観測者が見ると,ミユーオンの寿命が延びて観測されるのである。どのくらい寿命が延びるかというと,200倍にも逢する。 ところが,もしミユーオンの立場に立てば,寿命はちっとも延びないのだから,地上に届くはずがない,と思われるかもしれない。実際,だから相対論は間違いなのだという本を書いている大学教授もいる。しかし,簡単なことだ。ミユーオンの立場に立つと,確かに寿命は延びないが,進むべき距離が短縮されるのである。つまり大気の厚みが,たとえば200分の1に薄くなってしまうのである。だからどちらの立場に立っても,結論が異なることはない。それが相対論の神髄なのである。 |
可笑しくはありませんか?
松田氏は、“ミユーオンの立場に立つと,確かに寿命は延びないが”、“地上の観測者が見ると,ミユーオンの寿命が延びて観測されるのである。” と認識されているのは結構なのですが、“(ミユーオンの立場に立つと)……大気の厚みが,たとえば200分の1に薄くなってしまうのである。だからどちらの立場に立っても,結論が異なることはない。それが相対論の神髄なのである。”との結論は、『言語明瞭意味不明』のご発言のように感じます。
第一、松田氏は、「双子のパラドックス」の解説に於いて、“ロケットは方向転換のときに加速度運動をするということができる。するとこのときに,みかけの力が発生する。ところが弟には,兄の方向転換のときに,このようなみかけの力は発生していない。
だから二人の立場は対称的ではないのである。やはり弟と全宇宙が静止していて,兄はそれに対して運動していると考えるべきなのである。”だとしたら、和田氏の例の如く、ミューオンを加速器で加速した場合は、どうなるのですか?ミューオンには加速のための見かけの力が働くと解釈するなら、私達が静止していて、ミューオンだけが運動していると考える事になり、“どちらの立場に立っても,結論が異なることはない。それが相対論の神髄なのである。”とは言えなくなってしまいます。
更に、大気の厚みの変化と共に、ミューオンの寿命が異なるなら、その寿命が大気と共に作用、又、反応する事で決定されるが如くに受け取られます。
このような解説では、「訳の判らない解説をして煙に巻くのが、“相対論の神髄なのである。”」と感じてしまいます。
ここで、両先生のご高説は脇に於いて、先に掲げた「双子のパラドックス」の「ミュー粒子版」を考えてみましょう。
初め、ある空間に双子のミュー粒子がいて、兄のミュー粒子が、弟のミュー粒子に対して、光速度の99.94%で走り始めた場合を考えてみましょう。
弟から、兄の時計を見ると(先の和田氏の計算通りに)、約29分の一の速度で進むのが観察されます。そこで、兄の寿命は本来、十万分の一秒であったのが、その29倍の十万分の二十九秒と観察される事と期待されます。
最近はIT関係の技術進歩が激しくて、その進歩にはドッグイヤーという表現がされます。
即ち、「人間にとっての1年は、犬の年齢では7年に相当する」との背景から、「IT関係の1年間での進歩は、従来技術の7年間の進歩にも相当する。」との事だそうです。
ここで一寸話の展開を判り易くする為に、ミュー粒子の年齢の表記方法を、次のように「ミュー粒子イヤー」を導入してみましょう。
“我々通常の時計の(十万分の一秒)/29”=“ミュー粒子の一年”
このミュー粒子イヤーを用いて、通常のミュー粒子の寿命を、29μ歳と表記致します。
では、生れ落ちると直ぐに、光速度の99.94%で走り始めた兄の寿命(加速される前では二十九μ歳)は、どうなるのでしょうか?
(生まれて直ぐに走るのは人間の世界では不可能ですが、ミュー粒子の世界の出来事なので、この点は深く追求しないで下さい。
でもどうしても気になる方は、双子は同じような魔法のカーッペットに乗っていて、その一方の兄のカーペットが、光速度の99.94%で動き出したと考えて下さい。)
先ずは、取り残された弟から見た兄の寿命を考えてみましょう。
弟から兄の時計を見ると、弟の時計の二十九分の一の速度で動いているのを観察するでしょう。
ですから、弟自身の時計が29年経過していても、弟から見た兄の時計は1μ年しか進んでいないのです。
即ち、弟の29μ歳の寿命が尽きる時、弟から兄を見ると兄の年齢は1μ歳にしか見えていないでしょう。
(そこで、弟は兄に比べて余りにも早く寿命が尽きてしまう事を嘆くかもしれません。)
一方、光速度の99.94%で走り始めた兄から弟を見た場合はどうでしょう。
この場合『アインシュタインの特殊相対性理論』の世界(我々の世界でも、我々が電車に乗っていて、片方の電車が動き出した時、自分の乗ってる電車が動いたのか、隣の電車が動いたのかが判らないものです、ですから、自己中心的に自分の電車は止まっていて、隣の電車が動いたと認識するのが、アインシュタインの世界)では、兄は“自分は停止していて、弟が(弟が兄が走り出したと認識した方向の逆方向へ)光速度の99.94%で走り始めた。”と認識するでしょう。
このことから明らかなように、今度は先程の、弟と兄の立場がすっかり入れ替わる事になります。
即ち、弟の年がまだ1μ歳にしか見えないのに、兄は既に29μ歳となり、無念にも寿命が尽きてしまうのです。
これでは、この双子のミュー粒子の兄弟は、互いに寿命が尽きて天国へ言った際、お互いの年齢の話になると、意見が合わずに喧嘩になりかねません。
『アインシュタインの特殊相対性理論』の世界では、勿論、神様といえども「絶対的な時計」を所持出来ません。
そこで、優しい神様は、この双子のミュー粒子の紛争に対して、次のように仲裁するのかもしれません。
神様は、もう一度双子たちを生き返らして、再現実験をされるでしょう。
その際は、兄が光速度の99.94%で走り出したら、神様は兄の後から、兄の走る半分の速度(光速度の49.97%)で走り出します。
これによって、双子の兄弟は(方向は逆ですが)神様から、光速度の49.97%で離れてゆくのと等価となるのですから。
そして、神様から双子の兄弟の時計を覗けば、兄弟二人の時計は同じ速度で動いている事が観測されます。
ですから、神様はご自身の時計が、双子の時計の1/√(1-(0.4997c/c)2)=1.34倍早く進むと観測されます。
従って、双子が同時に彼等の29歳の寿命を閉じる時、神様がご自身の時計を御覧になると、
29×1.34=33.5μ年の経過を示しているでしょう。
そして、再度神様と双子は天国でお会いになって、神様は、“二人とも同時にお前達も確認したろうが、お前達の時計で29歳で、但し、私の時計で測ったら33.5μ歳で、お前達二人は同時刻に死んだんだよ。”と双子の仲を取り持たれるでしょう。
それでも双子が疑い深いと、まだ腑に落ちない顔をするかもしれません。
何故なら双子からは、神様の時計は、双子の時計の√(1-(0.4997c/c)2)=0.866倍の速度で動いていた結果、彼等が自分の時計で29μ歳の寿命を全うした時には、神様の時計は、29×0.866=25.1μ年しか経過していなかったのですから。
更に、神様ご自身も少し心配になりました。
“このような疑い深い双子の若干の不満は残したが、何とか、双子の仲を取り持つ事が出来たが、次には、三つ子達が別々の速度で走り出したら、彼等を如何に仲裁たら良いものか?”
と、お考えの処へ、別のミュー粒子の双子がやってきました。
今度は、兄の寿命(29μ歳)が尽きる前(例えば、兄の時計で20μ歳の時)兄の乗ったカーペットが、停止してしまったらしいのです。
その時、兄は弟の時計を覗くと、(なにしろ、兄から弟を見た時には、兄は停止していて、弟が走っていると認識するのですから、弟の時計はゆっくり進んでいて)、未だに、
20×0.866=17.3μ年
しか経過していない事に驚きました。
一方、弟から兄を見ると、兄が動いているのですから、兄の時計はゆっくり進んでいて、兄の時計が、20μ年を指した時点では、弟の時計は、
20×1.34=26.8μ年
となっている事を認識したのです。
こうした体験の後、又、この双子のミュー粒子は天国へ行き、神様を悩ませたのです。
そこで、神様は、又、再現実験をして下さいました。
それでも神様は、今後の事も考えて、今回は、兄のカーペットが動き出してから、弟の時計で20μ年が経過したときの状況を双子に報告させます。
今度は、先程の兄と弟の立場がすっかり逆転してしまいました。
弟が自分の時計で、20μ年経過したと認識した時、弟から見て動いていたと認識していた兄の時計は当然ゆっくり動いていたように見え、
20×0.866=17.3μ年
と認識します。
一方兄はというと、弟が弟の時計で20μ年と確認した時、兄は慌てて自分の時計を覗きます。
(この場合も、兄から弟を見た時には、兄は停止していて、弟が走っていると認識するのですから、弟の時計はゆっくり進んでいて)
20×1.34=26.8μ年
となっている事を認識しました。
この結果双子たちは却って混乱してしまいました
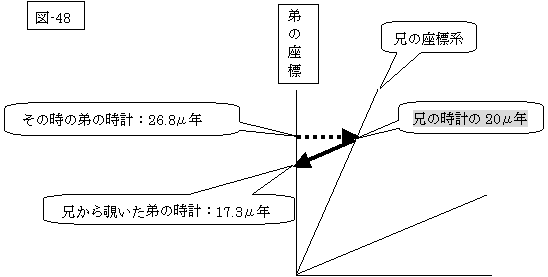
そこで、親切な神様は双子の為に、次表を作られ、また、図さえもつくられ、 “『アインシュタインの相対性理論の世界』では、兄の世界では同時刻に起こったことと兄が認識していても、弟から見ると同時刻には見えないのであって、同時刻という概念には絶対的な意味はなく,座標系によって異なる相対的な意味しかもたないのだ。”と諭されながら図の説明までもなさるのでした。
|
兄が自分の時計で20μ年と 認識して停止した場合 |
弟が自分の時計で20μ年と 認識した時停止した場合 |
|
| その時の弟の時計 |
26.8μ年 |
20μ年 |
| その時の兄の時計 | 20μ年 | 26.8μ年 |
| 兄から覗いた弟の時計 |
17.3μ年 | 20μ年 |
| 弟から覗いた兄の時計 |
20μ年 |
17.3μ年 |
 |
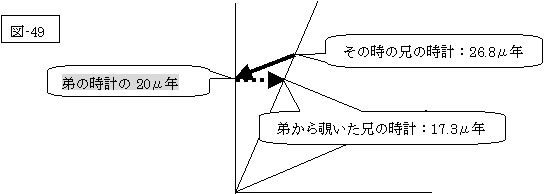 |
神様がこのように、“お互い立場によって対照的な結果になるのだよ。”と親切に説明されても未だ二組のミュー粒子の双子は怪訝そうな顔をしている上に先程の双子は、魔法のカーペットに乗ったままお互いに反対方向に飛んで行き、途中から同時にもとの位置に戻って来て、お互いの時計を見比べて口論を始めてしまいました。
そこで、神様は、今回は天国のアインシュタインに助けを求めました。
アインシュタインもローレンツの変換式を書いて、じっくりと次のように説明を始めました。
| ここで、K系(x、y、z、t)、から、K系の時計で、vの速度で遠ざかるK’系(x´、y´、z´、t´)を考えると、K系で、時間がt経過した時には、K’系は、K系から、x=vt だけ遠ざかっていることになるので 右の(t´=……)の式に、x=vtを代入すると、分子は、t(1-(v/c)2)となりますので t´=t√(1-(v/c)2)となるのです。 √(1-(v/c)2)は、明らかに、1より小さいのですから、ここで、多くの下界の物理学者達は、「動いている時計は遅れる。」と言う訳です。 |
x'=(x-vt)/√(1-(v/c)2) y'=y, z'=z t'=(t-(v/c2)x/√(1-(v/c)2) |
しかし、『我が相対性理論の世界』では、今掲げた2式(ローレンツの変換式)が示すように,ある座標系で時間(或いは、空間)と考えている量が、他の座標系でみると,時間と空間座標のまじり合ったものになるというのであるから、時間と空間の間にはもはや絶対的な区別はつけられない。そこで、両者を統一した時間・空間、または略して「時空」の概念を導入する事が重要なのです。”
従って、時間だけ取り上げて、“同時刻だ!?”“同時刻でない!?”と言うのは余り意味のある事ではないのです。
その好例を、先の図-48、図-49に示す事が出来ましょう。
図中の矢印に於いて、点線の延長線上は弟にとっての同時刻で、実線の延長線上が兄にとっての同時刻なのですから、この双子にとっての同時刻性を扱うのは難しくなります。
しかるに、自著『特殊および一般「相対性理論」について』(アルバート・アインシュタイン著、金子務訳:1998年9月31日:白揚社発行)の118頁に書いたように、ミンコフスキーは、“二つの事象あるいは二つの四次元の点〈距離〉と呼ぶ大きさ(四次元の時空連続体上の相近接する二点に属する大きさ=ds)が、選ばれたすべての(ガリレイ)基準体に対して同じ値をもつ。”
ds2= dx2+dy2+dz2-c2dt2 (=基準体の選択に無関係で、一定値を示す)
という簡単な条件をローレンツ変換が満足させる事を見つけています。
空間的には、通常x方向だけを考慮しているので、y、zは考慮せずとも、
ds2= dx2
-c2dt2 (=基準体の選択に無関係で、一定値を示す)
と書き換えることも出来るでしょう。
更に、下界では、主に「時間」の概念を問題にする事が多いので、下界で出版されている
『時空図で理解する相対性理論』(和田純夫著:1998.12.10:ナツメ社発行)の184頁には、「固有時間」の概念に変えて、(「固有時間」= c2dt2
- dx2 となるのですが、)ここに居るミュー粒子達にも、判り易く次のように書いてあります。
|
時空上の2点AとBを考える。一般にAとBは、位置も時刻も異なる。そこで、位置Aに時計を置き、時刻Aから動かし姶め、時刻Bに位置Bに到達したとする。その問に時計の針が進んだ時間を、2点A、B問の「固有時間」と呼ぶ。 このようにして時空上のさまざまな2点間に、固有時間というものが定義できる。これが、面上の距離に対応するものだ。 時計が動いていなければ、つまり位置Aと位置Bが同じ位置ならば、固有時間はもちろん、時刻Aと時刻Bの差である。しかし時計が動いているときは時間の遅れがあるので、固有時間はそれよりも短い。 では、固有時間はどのような式で計算すればいいだろうか。距離を計算するときに使えるのがピタゴラスの定理であったように、固有時間を求めるときに使うのが、次のミンコフスキーの定理である。 その定理によれば、 (AB間の固有時間)2=(AB間の時間の差)2−(AB間の位置の差÷c)2 |
我輩が、この「固有時間」を用いて、この先も解説を続けると、ここの双子のミュー粒子達の頭が理解出来ないかもしれないので、下界に居る「宇佐美」に、説明を続けさせましょう。
7.)ミュー粒子(ミュー(μ)オン)の寿命の「固有時間」を用いての解釈
以上のような天上での会話を夢の中で聞いた私は、喜んで又、「固有時間」を用いての説明を続けさせていただこうと存じます。
それにはもう一度先に神様が書かれた、図-48、図-49を一般化した図を書きたいと存じます。
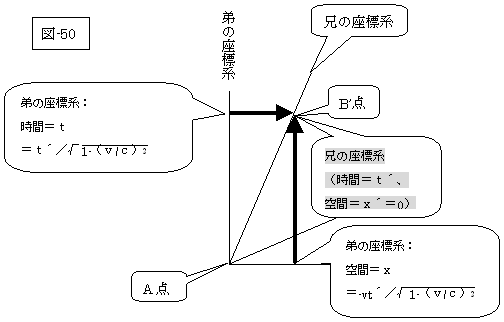 |
この図-50に於いては、一般的には、弟が静止していて兄が速度vで移動している時空図とみなせます。
そして、弟の座標点(t、x)を求めるにあたって、先の天国のアインシュタインが書かれた(次に再度書きますが)ロレンツの変換式(t´=……、x´=……)のtとxとを、そっくり其の侭書き変えて、次の式を用いるのです。
(この一寸不思議な操作が可能なのは、ロレンツの変換式『アインシュタインの特殊相対性理論の世界』に於いては、K’系(t´、x´)からK系(t、x)を見ようが、K系からK’系を見ようがその関係は同じなのですから。但し、速度は+vから-vに変わります。)
| x=(x'+vt')/√(1-(v/c)2) t=(t'+(v/c)2x')/√(1-(v/c)2) |
図-50における(AB’間の固有時間)2=(AB’間の時間の差)2−(AB’間の位置の差÷c)2
を、兄のK’系と、弟のK系について各々計算してみますと、
(但し、(時間の差=t´)(位置の差=x´=0))
|
兄のK’系では、(AB’間の固有時間)2 =(AB’間の時間の差)2−(AB’間の位置の差÷c)2=(t´)2、 弟のK系では、(AB’間の固有時間)2 =(AB’間の時間の差)2−(AB’間の位置の差÷c)2 =〔t´/√(1-(v/c)2)〕2-〔(v/c)t´/√(1-(v/c)2)〕2 =((t´)2-(vt´)2)/(1-(v/c)2) =(t´)2(1-(v/c)2)/(1-(v/c)2)=(t´)2 |
となり、兄も弟のどちらの系でも、B’点の「固有時間」は共に、兄の系の時間「t´」と等しい値を示すのです。
(即ち、兄が、兄の系で感じた時間が、其の侭兄の時空の「固有時間」に合致するのです。)
次の図-51にて、弟の(A点からB点までの)時空についての「固有時間」を計算してみましょう。
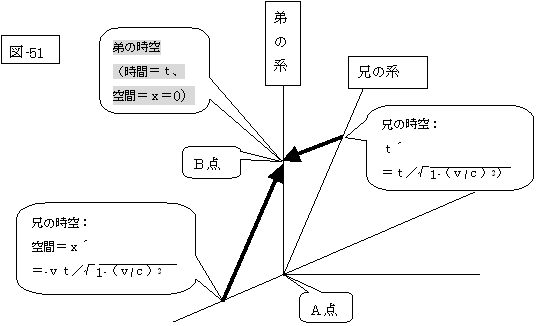 |
この図-51に於いては、一般的には、兄が静止していて弟が速度-vで移動している時空図とみなせます。
そして、先程と同じように、上図の兄と弟の系に於いて各々「固有時間」を計算しますと、共に、「固有時間」が弟の系での時間「t」である事が判ります。
かくして、A点からB点の「固有時間」は、双子の兄弟は、初め両者の原点(A点)に位置して、ある時間が経過した後の認識の対象が存在する位置(B点)が、兄の系(K’系)に存在にした(認識の対象が兄の場合)(図-50)か、弟の系(K系)に存在(認識の対象が弟の場合)にした(図-51)か、によって異なり、K’系では「t´」になり、又は、K系では「t」になります。
更に、ミュー粒子の寿命を「固有時間」で、観測してみましょう。
先ず、先の図-50を見て、双子のミュー粒子がA点で生れ落ちた直後、自分は停まっていると認識している弟から見て、兄のミュー粒子が速度vで、時間t´移動して、B´点まで移行したとすると、A点からB´点までの「固有時間」を、兄と弟の各々の座標系で計測してみましょう。
(AB間の固有時間)2=(AB間の時間の差)2−(AB間の位置の差÷c)2
先ずは、兄の座標系では、AB間の固有時間=t´となります。
何故ならば、 AB間の時間の差=t´ AB間の位置の差÷c=0 なのですから。
弟の座標系では、 AB間の時間の差=t´/√(1-(v/c)2)
AB間の位置の差=-vt´/√(1-(v/c)2) ですから、
(AB間の固有時間)2=(AB間の時間の差)2−(AB間の位置の差÷c)2
=((t´)2-(vt/c)2)/(1-(v/c)2)=(t´)2(1-(v/c)2)/(1-(v/c)2)
=(t´)2
従って、弟の座標系でも、AB間の固有時間=t´となるのです。
ですから、兄のミュー粒子の寿命を「固有時間」で観測すれば、認識の対象となる兄は、兄自身の座標系に存在しているのであるから兄の寿命が尽きたときの兄の時間が、その「固有時間」となるのです。
従って、地上の我々が如何にミュー粒子を加速しても、加速されたミュー粒子自身は、(決して我々の座標系に存在するのでなく)ミュー粒子自身の座標系に存在しているのですから、物理学者達は、「ミュー粒子の寿命を伸ばした!」と騒いでも、それはあくまでも地球の時間で測定した寿命でしかないのです。
どんなにミュー粒子を加速しようとも「固有時間」でミュー粒子の寿命を観測するならば、不変なのです。
ここまでの話を夢の中で、天国のアインシュタインに報告したら、天国のアインシュタインは、「宇佐美よ、ここまで理解出来たのなら、下界の物理学者のほとんど全てが誤解している“双子のパラドックス”に対して、(一般的な条件で、)もう一度「固有時間」を用いて解説してみたらどうか?」と、又、“何故、「固有時間」を用いての説明が明快になるかの理由も説明するように!”とおっしゃって下さいました。
8.)“双子のパラドックス”に対しての「固有時間」を用いての解釈
地球上から、双子の兄が宇宙船に乗って宇宙旅行に出発し帰って来るのを、地球上の弟が地球の座標系で観測すると、“速度vにて時間tの間、地球から離れて行き、その後、又、時間tを費やし速度vにて地球へと帰って来た。”と表現出来ましょう。
(勿論、ここでの双子も、地球と宇宙船に拘らず、先程の双子のミュー粒子のように双方魔法のカーペットに乗っていても良いのです。))
この現象を、地球上の弟と、宇宙船の兄との座標系で解釈しようとすると、先の図-30、図-31、図-32に示した如く、兄の宇宙旅行中、地球上の弟をに停止していたと解釈すれば、弟の座標系は、兄の宇宙旅行の初めから終わりまでを一つの座標系で表せますが、兄の場合は、図-31、図-32の如くに、行きの場合と帰りの場合の二つの座標系に分かれてしまいます。
そこで、兄を一つの座標系で表記するには、次のような二つの座標系を考慮すると良いのです。
一つの座標系は地球に留まる弟の属する座標系(S系)、もう一つは兄の宇宙旅行の開始と共に地球から速度vで遠ざかる座標系(S’系)です。
そこで兄は、宇宙旅行の開始から地球の時間tまでの間は、このS’系の位置(x’=0)を離れる事はなく、折り返し点についた後、再び兄は、又、地球の時間tで、このS’系の中を(S’系で測定した新たな速度uで、)地球へと帰還するのです。
ここで、兄の帰還時のS’系の中での新たな速度uが、突然出てきましたが、この速度は如何なるものかを計算します。
先ず、兄の帰還時の速度を地球上の弟から観測すれば、当然、兄の出発時の速度vとおなじで、かつ方向が逆の速度-vを観測するでしょう。
然るに、『なっとくする相対性理論』(松田卓也、二間瀬敏史共著)の83頁を参照しますと、
|
S系に対して,x軸の正の方向に速度vで運動しているS′系を考える。 そのS′系に対して速度uで運動している粒子を考える。…… また,粒子の速度をS系で測るとwになるとする。すると, w=(u+v)/(1+uv/c2) (c=光速度) |
と書かれていますから、上式での、「w」を「-v」と置き換えて、uを求めればよいのです。
即ち、-v=(u+v)/(1+uv/c2) から、uが求まります。
この式からuを解きますと、u=-2v/(1+(v/c)2) が得られます。
ここで、双子の兄弟が属する二つの座標系S、S’ を描いてみましょう。
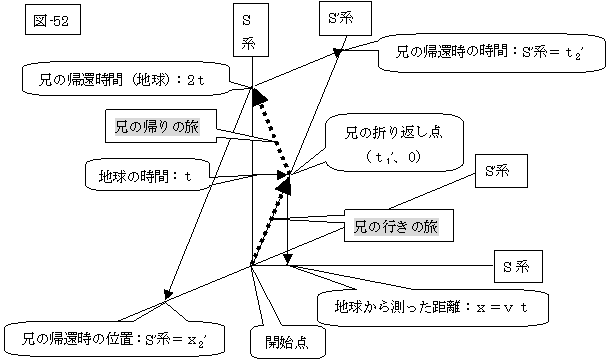 |
そこで、上表の不明部分をロレンツの変換式を用いて求める。
t1’ =(t-(v/c2)vt)/√(1-(v/c)2)=t√(1-(v/c)2)
t2’= 2t/√(1-(v/c)2)
x2’ =-2vt/√(1-(v/c)2)
よって、先の表を完成させますと、
| S系(弟の属する系) | S'系(兄の属する系) | |||
| 時間 | 位置 | 時間 | 位置 | |
| 旅行開始点 | 0 | 0 | 0 | 0 |
| 折り返し点 | t | vt | t√(1-(v/c)2) | 0 |
| 旅行終了点 | 2t | 0 | 2t/√(1-(v/c)2) | -2vt/√(1-(v/c)2) |
ここで、念のために、兄の属する座標系(S’系)での兄の帰りの宇宙船の速度が、先程、相対論における速度の合成式で求めた値と、今回求めた、兄の各時点でのS’系での座標値から計算した値と合致するかを確認します。
即ち、この座標値から求めた、兄の帰りの所要時間(T’)は、
T’= t2’-t1’=t(1+(v/c)2)/√(1-(v/c)2)
そして、兄の帰りの飛行距離(L’)、
L’= x2’ – 0=-2vt/√(1-(v/c)2)
従って、兄の帰りの宇宙船の兄の属する座標系(S’系)での飛行速度(u)は,
u=L’/ T’=(-2vt/√(1-(v/c)2))/(t(1+(v/c)2)/√(1-(v/c)2))
=-2v/(1+(v/c)2)
となり、先程の速度合成式から求めた速度と合致いたします。
この事は、今回私が、“地球(弟)の属する座標系(S系)と、地球から速度vで遠ざかる座標系(S’系)を考え、兄は常にこのS’系に属しており、折り返し地点からはその座標系の中で、速度uで地球に帰還する。”との設定が有効であった事を証明すると思います。
くどいようですが改めて書きますと、兄の宇宙旅行の行き帰り中、弟は常にS系に属し、兄は常にS’系に属していたのです。
先ずは、兄の出発点から、折り返し点までの「固有時間」を計算してみましょう。
弟の座標系で求めますと、
(固有時間)2=(時間の差)2−(位置の差÷c)2
=(t-0)2-(vt/c-0)2=t2(1-(v/c)2)=(t1’) 2
兄の座標系で求めても、
(固有時間)2=(t√(1-(v/c)2) - 0)2-(0-0)2=t2(1-(v/c)2)=(t1’) 2
と同じ固有時間になります。
次には、折り返し点から帰還時までの「固有時間」を計算してみましょう。
弟の座標系から、
(固有時間)2=(t-2t)2-(vt/c)2=t2(1-(v/c)2)=(t1’) 2
兄の座標系からは、先程、uを求める際に(時間の差)、(位置の差)を求める際に計算しましたので、それを利用いたしまして、
(固有時間)2=t2((1+(v/c)2)2/(1-(v/c)2)-(4t2v2/c2×(1-(v/c)2) =t2(1+2(v/c)2+(v/c)4-4(v/c)2)/(1-(v/c)2)
=t2(1-(v/c)2)2/(1-(v/c)2)=t2(1-(v/c)2)=(t1’) 2
先の説明(図-52)では、S系を「地球」、S’系を「行きの宇宙船の座標系」にしましたが、今回は、S’系を「帰りの宇宙船の座標系」(次図の図-53)にしても、同様の結果になります。
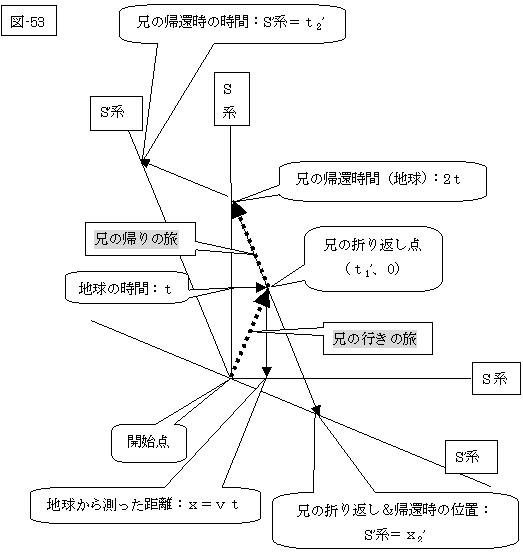 |
この場合は、「兄の行きの座標系」の移動速度(=v)に対して、「兄帰りの座標系」の場合はその移動速度を「-v」に置き換えて、ロレンツ変換を行えば、「兄の帰りの座標系」での座標点(t’、 x’)が下表の如くに求まります。
| S系(弟の属する系) | S'系(兄の属する系) | |||
| 時間 | 位置 | 時間 | 位置 | |
| 旅行開始点 | 0 | 0 | 0 | 0 |
| 折り返し点 | t | vt | t(1+(1+(v/c)2)√(1-(v/c)2) | 2vt/√(1-(v/c)2) |
| 旅行終了点 | 2t | 0 | 2t/√(1-(v/c)2) | 2vt/√(1-(v/c)2) |
ここで先程同様に、兄の出発点から、折り返し点までの「固有時間」を計算してみましょう。
弟の座標系では、先と同様に
(固有時間)2=(時間の差)2−(位置の差÷c)2
=(t-0)-(vt/c-0)=t2(1-(v/c)2)=(t1’) 2
兄の座標系では、
(固有時間)2=(t(1+(v/c)2)/√(1-(v/c)2))2-(2vt/√(1-(v/c)2))÷c)2
=t2((1+(v/c)2)2-4(v/c)2)/(1-(v/c)2)
=t2(1-(v/c)2)2/(1-(v/c)2)=t2(1-(v/c)2)=(t1’) 2
と同じ固有時間になります。
次には、折り返し点から帰還時までの「固有時間」を計算してみましょう。
弟の座標系では、これも先程同様に、
(固有時間)2=(t-2t)2-(vt/c)2=t2(1-(v/c)2)=(t1’) 2
兄の座標系では、
(固有時間)2=t2(4t-(1+(v/c)2)2/(1-(v/c)2
=t2(4(v/c)2-1-2(v/c)2-(v/c)4)/(1-(v/c)2)
=t2(1-(v/c)2)2/(1-(v/c)2)=t2(1-(v/c)2)=(t1’) 2
ここまでの計算でお分かりのように、「旅行出発から折り返し点」そして、「折り返し点から旅行終了点」までの「固有時間」を計算するにあたっては、「宇宙船の行きの座標系」を用いても、「宇宙船の帰りの座標系」を用いても全く同じ、それぞれの座標系での時間(t1’)になるのです。
この事は、「旅行出発から折り返し点」を「宇宙船の行きの座標系」を用いて、「折り返し点から旅行終了点」を「宇宙船の帰りの座標系」と二つの座標系を用いて同様な結果が得られるのです。
前記の「固有時間」は、兄が宇宙旅行をしていると見なして、その「旅行開始点→折り返し点→旅行終了点」の「固有時間」を計算しましたが、次には、地球に留まっている弟の「兄の旅行開始点→(弟は折り返し点には行かずに地球に留まったまま)→旅行終了点」即ち、「旅行開始点→旅行終了点」の「固有時間」を計算致します。
この結果、次のように「地球上で留まっている弟の時間」が得られます。
弟のS系に於いては、
(固有時間)2=(2t)2−(0)2
∴ 「固有時間」=2t
兄のS’系においては、
(固有時間)2=(2t/√(1-(v/c)2) )2−((-2vt/√(1-(v/c)2))÷c)2
=(2t)2(1-(v/c)2)/(1-(v/c)2)=(2t) 2
∴ 「固有時間」=2t
ここまでの事から判ります事は、“ある現象が、ある座標軸の時間軸に留まったまま進行したならば、その現象の「固有時間」は、その対象となる時間軸での測定時間に他ならない。”という事です。(∵ 時間軸上は、位置座標値は常にゼロですから。)
勿論、以上の考察は、当然のことながら、S系を宇宙船(この場合の宇宙船は、開始点から終了点まで不動で、地球が旅をすると考える。)、S’系を地球(の行きの場合と、帰りの場合の2種類)として考えても同じ結果が得られるのです。
(勿論、「旅行開始点→旅行終了点」の「固有時間」を計算する場合は、兄が宇宙船で留まっており、弟が地球での行き返りの旅をしている事になります。)
ですから、地球から見た時間だけを単独で取り上げて、宇宙船に乗って高速度で移動すれば、若くなるなどと解釈するのは誤解に基づいているのです。
それに、今回の計算結果では、旅行終了点の時間:t=2t、t2’= 2t/√(1-(v/c)2)、だけを比べると、従来多くの物理学者達が述べる宇宙船で移行する兄の時間は小さくならずに大きくなっているのです。
(∵ t2’/t2=(2t/√(1-(v/c)2)/2t)=1/√(1-(v/c)2)>1)
(但し、宇宙船が折り返し点まで行く時間だけを比べれば、従来から言われている通りに、兄の時間の進行は遅いのです。
∵ t1’/t1=t√(1-(v/c)2)/t=√(1-(v/c)2)<1)
これらの「時間」や「固有時間」については、次章移行でも論を進めます。
9.)「?の時間」は「空間の時間」
ここまで論を進めて来ましたが、たとえ「固有時間」を用いても、宇宙旅行の時間を、地球にしろ宇宙船にしろ、どちらの方に所属しようが、自分が動かずに留まっていたと認識してしまう方の「固有時間」が、tであって、動いている方としてしまった方の「固有時間」がt’と言うのでは、なにか先に言い出したほうに時間の選択権があるような可笑しな話が残ってしまう感じがします。
何故留まっていると認識した方の「固有時間」がtで、動いているとした方の「固有時間」がt’と両者に相違が出てきてしまうのでしょう。
更にこの点についての論を展開する前に、もう一度「旅行開始点→折り返し点→旅行終了点」の「固有時間」の件に言及しましょう。
この「固有時間」を求める際に、「旅行開始点→折り返し点」の「固有時間」を「宇宙船の行きの座標軸」、「折り返し点→旅行終了点」の「固有時間」を求めるのに、「宇宙船の帰りの座標軸」と混用して求めても、「旅行開始点→折り返し点→旅行終了点」の全行程の「固有時間」をどちらか一方で求めようと、同一である事を計算で証明しましたが、この際混用する座標軸の原点を平行移動して考えてみましょう。
この時、ある座標軸で「固有時間」を求める際に、この座標軸を、時間の軸、位置の軸をそれぞれ平行移動しても、求める「固有時間」には変化は生じないのです。
何故ならば、(固有時間)2=(時間の差)2−(位置の差÷c)2に於いて、「時間の差」、「位置の差」の所謂「差」の中に、座標軸の平行移動分が吸収されてしまうのですから。
∵ (t、x)→(t−α、x−β)の時、(但し、α、βは任意の定数)
「時間の差」=(t2−α)−(t−α)=t2−t1
「位置の差」=(x2−β)−(x1−β)=x2−x1
そこで、「旅行開始点→折り返し点」迄は、「宇宙船の行きの座標軸」で且つこの座標軸の原点は宇宙旅行の出発点(地球系の原点に同じ)、「折り返し点→旅行終了点」迄は、「宇宙船の帰りの座標軸」でありながらこの座標軸の原点を、旅行の折り返し点と合致させます。
この結果、次図(図-54)が得られます。
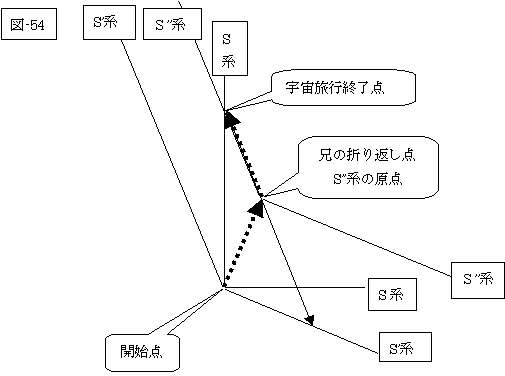 |
この結果、次の図-55が得られるのです。
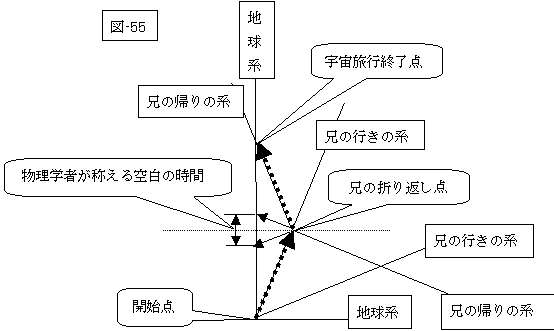 |
この図には、当然先に和田氏らの物理学者達が忌み嫌って避けてきた「?の時間」「失われた時間」「空白の時間」等と名付けられた不思議な時間が姿を現します。
でも、ちっとも怖くも困った存在でもないのです。
また、「?の時間」等と、回避しなければならない存在ではないのです。
この事は、今まで記述して来ました「固有時間」の本質をご理解頂ければ、誤解し続ける物理学者達が「?の時間」等と勝手に名付けてしまっている「時間」は、「時間」でなく「位置」(位置的時間)なのです。
図−55の兄の旅行の過程(矢印の軌跡)を辿って頂ければ、行きも返りも座標軸の時間軸(位置=0)をたどっている事にお気付きでしょう。
この結果、「固有時間」の計算の際には、「時間」部分のみになり、本来存在していた「位置」部分が欠落したように見えます。
この「位置」の欠落部分が、いわゆる「?の時間」に相当するのです。
ですから、この「?の時間」部分は、存在してしかるべきなのです。
物理学者達が誤解し続けるこの「?の時間」は、実は「空間の時間」なのです。
ですから、図-55での宇宙船の速度を変化させれば、宇宙船の折り返し点の位置(地球から)は、変化して、その変化の量につれて、この「?の時間」即ち「空間の時間」が変化するのです。
そして、宇宙船の速度が低下してゼロになってしまえば、宇宙船は地球に留まっている事になりますから、折り返し点の位置は地球上ですから、「?の時間」即ち「空間の時間」も、ゼロになります。
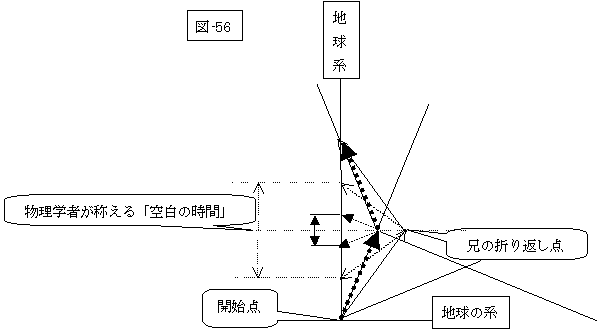 |
しかし、誤解する物理学者達は、“双子の兄が、折り返し点で、行きの座標から、帰りの座標へ乗り換えるのは、特殊相対論の領域ではない!”と喚かれるかもしれませんが、それではそもそも、兄が宇宙旅行へ出発する際は、地球の座標から宇宙船の行きの座標へ何の不思議も無く乗り換えているではありませんか!?
だとしたら、折り返し点でも、座標軸を乗り換えてなんら支障が有りましょうや!?
10.)実際には、どちらの双子が年を取ったか?
図−55での座標系での宇宙旅行の全行程の時間の推移を追って見ますと、次表が得られます。
| 地球系 | 旅行行き系 | 旅行帰り系 | |
| 旅行開始点 | 0 | 0 | |
| 折り返し点 | t | t√(1-(v/c)2) | |
| 旅行終了点 | 2t | t√(1-(v/c)2) |
この場合の旅行全行程の時間を地球に残った弟の時間と、旅行をして来た兄の時間とを比べますと、前者では:2t、後者では: 2t√(1-(v/c)2)=2t’
この時間の関係は言うまでも無く、停止している系の時間(2t)と、その系からvの速度で遠ざかる系の時間(2t’=2t√(1-(v/c)2))の関係である事が判ります。
但し、この場合は、空間座標は、前述の通りに常にゼロのままです。
しかるに、一般的には、ロレンツ変化の式
t’=(t-(v/c)2x)/√(1-(v/c)2)
を持ち出すまでも無く、時間の中に空間座標も同じように入ってきてしまうのです。
従って、空間座標(x)がゼロの場合のみ、時間だけを比べる事が可能なのです。
ですから、図−55の場合を検討したいのです。
(この図−55の場合と異なり、図−53の場合は折り返し点から旅行終了点までは、宇宙船の空間座標がゼロから離れる為に、旅行全行程の時間は2t/√(1-(v/c)2)の時間を示してしまうのです。)
そして、今回(図-55)の場合、旅行全行程の「時間」には空間項が無い為に、この旅行全行程の「固有時間」とも等しくなるのです。
ですから、逆説的に言いますと、時空図において時間を観測するには、何も「空間項」の無い経路となるようにわざわざ座標軸を平行移動せずとも、すんなりと「固有時間」にて観測することで事が足りるのですから、「固有時間」にて観測すべきなのです。
更に、今まで話してきましたように、和田氏の「?の時間」や、松田氏の「加速度の問題上、宇宙船のみが動き、地球は常に留まっている。」等という、とんでもない呪縛から開放されているのですから、弟と兄の立場を反対にしても良いのです。
即ち、宇宙船の兄が留まっていて、兄からvの速度で、地球上の弟が地球と共に宇宙旅行を体験してきたとしても、この関係は成立するのです。
即ち今度は、兄の時計は2tで、弟の時計は2t√(1-(v/c)2)=2t’と見えるのです。
但しこの場合(ある方向に進んだ後、元の位置に戻ってきた場合)は、先に掲げた(図-50)(図-51)の一方向のみに移動するミュー粒子の寿命の場合と違って、K系K’系を静止系、運動系と自由に選択が出来ないのです。
なにしろ、(図-53)、(図-54)では、旅行終了点に於いては、弟は弟の座標軸の時間軸上(位置=ゼロ)に居りますが、兄は兄の座標軸の時間軸上(位置=ゼロ)には居ないのですから、兄を静止した場合を想定できないのです。
そこでこのような場合は、改めてK系を静止系、K’系を移動系として、兄弟を配置し直さなければならないのです。
(兄の宇宙船が停止していると見なす為には、兄をK系に配置し直さなければならないのです。)
しかし、又、兄を行き帰りと別の座標軸に分けて兄が常に兄の座標系の時間軸に配置した場合(図-53)では、弟の座標系に前述の「空間の時間」が発生しますが、この点を考慮すれば、(図-53)の場合には、K、K’系どちらを静止系に見立てても、静止系と見なした方の「固有時間」が、tとなり、移動した系の「固有時間」が
t’=t√(1-(v/c)2)と観測されるのです。
かくして、兄弟共々、相手が宇宙旅行をして来ようが関係なく、自分の年は、自分の時計で見る通りに年をとっているのです。
(なにしろ、自分の時計を自分で見る際は、「アインシュタインの特殊相対性理論の世界」では、自分が停止して、相手が移動していると認識しているのですから。)
但し、相手側の年は、あくまでも動いている時計に基づいて、時の刻みが遅いように見えるのです
そして、その遅くなった分は、「固有時間」に見られるように「空間の時間」なのです。
即ち、“動いている系の時計は遅れる”を言葉を変えれば“動いて位置を変えた系はその位置の分時間が遅れる。”
11.)ミュー粒子の寿命で具体的に考えましょう
ミュー粒子の寿命を、先程の「ミュー粒子イヤー」を少し変形して導入してもう一度考えてみましょう。
即ち、“我々通常の時計の十万分の一秒”=“ミュー粒子の一年”=1μ年
として、ミュー粒子イヤーでは通常のミュー粒子の寿命は、1μ歳と表記できるとしました。
単純に、ミュー粒子を一方向にv=0.9994cに加速した場合は、
ここで、ロレンツの変換式を用いて、
地球から覗いたミュー粒子の時計=1μ年/√(1-(v/c)2)=1×29=29μ年
(∵ v/c=0.9994のとき 1/√(1-(v/c)2)=約29倍)
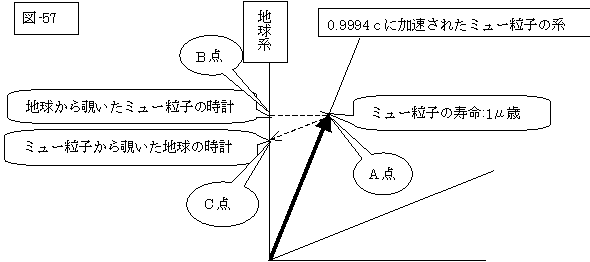 |
又、ミュー粒子から覗いた地球の時計は、地球系の座標が(時間=t、空間=0)に対して、ミュー粒子系の座標が(1μ年、0)となるような時間tをロレンツの変換式から求めると、
ミュー粒子から覗いた地球の時計=1μ年×√(1-(v/c)2)=(1/29)μ年
このように、ミュー粒子の一年の寿命に際し、地球から見ると動いているミュー粒子の時計がゆっくり動いているように見えて、あたかもミュー粒子の寿命が29倍伸びたように観察されますが、ミュー粒子から見れば地球が動いているように見えるので、ミュー粒子の命(ミュー粒子の時計で1μ年)が尽きる時、地球の時計は(1/29)μ年しか経っていないように見えるのです。
次には、図−55のように地球に対して往復した場合を考えましょう。
但し、ミュー粒子の寿命が1μ年しかないので、半μ年経ったら折り返し点から地球に戻ってくるとします。
この時の全旅行中の時間を地球で測った場合と、宇宙船で測った場合とで導き出したように
前者の場合が2t、後者の場合が2t√(1-(v/c)2)
そして後者の値を1μ年としますと、前者の2tの値は29μ年となります。
(∵ √(1-(v/c)2)=1/29)
しかし、この図-55の行って帰って来るの場合では、図-58の行ったきりの場合と違って
ミュー粒子の1μ年の旅の相対的な旅行として、ミュー粒子自身が停止していて、地球が宇宙旅行した場合のミュー粒子から覗いた地球の時間が見られません。
そこで、図-58をもう一度良く見て頂きますと、A点はミュー粒子の1μ年の旅の終了時です、
B点はその旅の完了時を、静止している(我々が)地球から見ている時空点です。
さて、C点ですが、これは何とミュー粒子がその寿命の1μ年間ミュー粒子の場で静止してそのμ粒子系での同じ時間、逆に地球(観測している我々)が、ミュー粒子からv(=0.9994c)の速度で遠ざかった場合の時空点なのです。
(ですから、その時空点の「固有時間」は、μ粒子の時間から、この地球が遠ざかった移動距離分に相当する「空間時間」を差し引いかれて遅れた時間が観測されます。
勿論、この同じ点(C点)の地球系での空間座標はゼロですから、「固有時間」は、その点での地球系での時間に等しくなります。)
即ち、図−58の場合は、相対論的にミュー粒子、地球のどちらでも静止の立場で相手の時間(自分の時間も)を観測することが出来るのです。
でも、図−55の場合には、静止続ける地球は位置の変化がありませんが、旅行するミュー粒子は時空図の中で折り返し移動をしている為に、位置の変化が発生します。この変化分を図−56では(「?の時間」ではなくて)「空間の時間」と説明しました。
また、図-55と等価の図−53,54で位置の相違がより鮮明に確認されます。
そこで、ミュー粒子が停止して地球が逆に移動する時空図は、図−55では、両者の立場を入れ替えた時空図に書き換える事が必要です。
即ち、今度は地球が折り返しの旅行をするのです。
この結果ミュー粒子の寿命の1μ年(=2t)での、
地球の旅行時間(=2t√(1-(v/c)2))は、(1/29)μ年と観測されるのです。
何度も何度も繰り返し書きますが、空の星々から我々地球を見たら、我々地球は高速度で移行しているのです。
なのに私達の寿命は全く変化していないと我々は認識しているのです。
万一、我々の寿命が、空の星々から我々地球を見る事で我々の寿命が変化したら大変です。
なにしろ、星々の移行速度は皆まちまちなのです。
このまちまちの速度で移行する星々から我々地球が覗かれたら、我々の寿命はめまぐるしくまちまちに変化してしまうのですから。
ですから、様々な速度で宇宙を移行する星々から見た我々地球との関係を、上式で見るならば、tが我々自身が地球で認識している時間で、t’が星々から我々地球を覗いたときに我々の時計の進行を認識する時間なのです。
時間t’は、星々が勝手に覗いて勝手に感じた時間なのです。
12.)夢の中での天国のアインシュタインのお話
以上の話を、夢の中で天国のアインシュタインに報告しましたら、天国のアインシュタインは、「フムフム」と頷かれ、次のように語り始めました。
“下界では、物事を表面的に理解する人間達が大多数で、その本質を理解する人間が少ない。
我輩が独自で導き出した座標変換式(下界ではローレンツの変換式と言っているようだが)に基づいて、ローレンツ達は「動いている物は、寸法が縮み、時間も縮まる。」と解釈していたのに、我輩は、「動いている物は、寸法が縮むように見え、時間も縮まるように見える。」と解釈したのである。
この「縮む」と認識するのと「縮むように見える」と認識するのとは大変な違いであって、この認識の相違こそが我輩の業績の根幹をなしているのに、この相違に無頓着な輩が余りにも多すぎる。
この「縮む」と「縮むように見える」が全く異なるのに、この点を同じと混同してしまうのには、呆れ果ててしまうのだ。
この結果J・Sベルなる物理学者が提起した、「細い紐で結んだ2台のロケットのパラドックス」等も、「寸法が縮んで見える」を「寸法が縮む」と誤解するから、「2台のロケットを結んでいる紐が2台のロケットが同時に出発した際でも切れてしまう。」と誤解してしまうのだ。
その上、下界での世界の一流の物理学者が集まっていたCERNにおいて、この問題は侃侃諤諤の議論を引き起こし、たった一人「ひもが切れるなどという世迷い事をいう奴は相対論がまったくわかっておらんのじゃ」と怒り心頭に達した高名なノーベル賞学者いたそうだが、若しその学者が天国に来たら、或いは来ていたら、早速、彼を称え慰めて上げよう。
更に、ミュー粒子を地球上で加速しようが、地球上の人間からは「恰もミュー粒子の寿命が伸びたように見える。」が、だからといって、「ミュー粒子自身が認識する寿命は伸びていないのだ。」
そして、このミュー粒子の寿命を「固有時間」で認識するなら、ミュー粒子自身は加速されようが常に、ミュー粒子はミュー粒子の座標系の位置がゼロの位置に存在し続けると認識出来るので、「固有時間」は、常にミュー粒子の時間そのものとなる。(勿論、地球の人間から観測しようとも。)
この事は、宇佐美が繰り返し例にあげている、「空の星々と地球上の時間の関係」と同様である。即ち、星々が様々な速度で地球から離れて行こうとも、それら星々と地球との間で、地球上でのある時間間の「固有時間」を認識するなら、ミュー粒子の場合と同様に、地球(地球上の人間達)は、常に地球の存在する座標系の位置がゼロの位置に存在し続けると認識出来るので、ある時間間での「固有時間」は、どのような星々から認識しようとも、「地球上での時間」に合致する事になる。
我輩の業績の基礎は、我輩が常に行った「思考実験」であった事は、下界の人間は知っていそうなものなのに、残念ながら彼等は我輩の残した数式ばかりに囚われて、とんでもない隘路に陥ってしまう。
こんな事だから、若しも、我輩が下界で『特殊相対性理論』を残してこなかったら、誰一人として、今もって、この理論を完成出来た者は居ないと思うよ。
だから、そんな下界で誰も認めてくれないといって嘆いてはいけないのだ。”との天国のアインシュタインのお言葉を聞いている内に、私は目が覚めてしまいました。
(補足−1)回転時空図で『双子のパラドックス』を考えてみましょう。
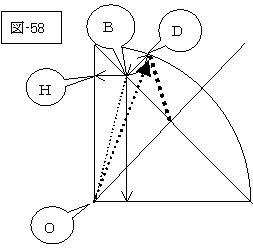
双子の弟が地球に留まり、地球時間(速度:V、時間:T)で、兄が宇宙船に乗って、折り返し点まで行く時空図は、丁度図-58に於いて、OHが地球の弟、OD(OB)が宇宙船の兄の軌跡を表している事になるでしょう。
 |
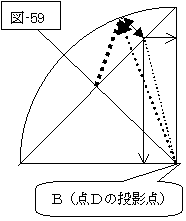 |
そして、宇宙船が折り返し点到着後は、時空面と光軸の関係は、宇宙船が地球に接近するので、光軸が90度展開した図-59の状態となり、宇宙船は地球に帰ってきます。
勿論、帰って来たといっても、時空面はズレてしまっており、投影面上で帰ってきただけです。
参考の為に、図-58と、図-59を合体しますと、図-60のようになります。
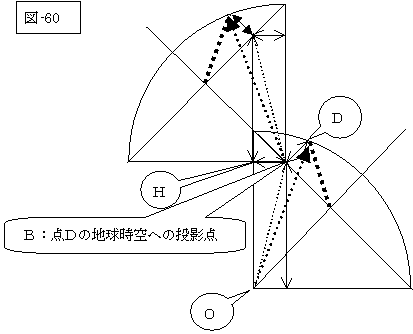 |
そして、この図からも判りますように、地球の弟と宇宙船の兄の立場(時空面上での立場)を変えても同じ関係にあるのです。
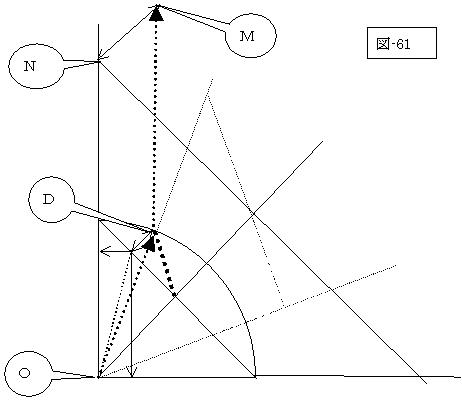 |
即ち、宇宙旅行後に双子の兄弟が地球上で顔を合わせても、それは、時空面上での観点から言えば、実態同士が対面しているのでなく、互いに相手方を自らの時空に投影した影と対面しているのです。
そして、自らの時空に投影する際には、相手側の虚時間分(?)が消滅してしまうのです。従って、相手方の年が若く見えても当然なのです。
今述べた説明では、地球の座標系がK、行きの宇宙船の座標系がK’、更に、帰りの宇宙船の座標系がK’’との関係でしたが、これを図-67のように考えます。
すると、宇宙船の座標系をK’のままで、宇宙船は帰りの速度は、地球からはマイナスVに見えますから、先程の(5式)に於いて、W=-Vと置き、K’系での帰りの宇宙船の速度(U)を求めますと、
W=(U+V)/(1+UV)…… (5式)
∴ U=-2V/(1+V2)
従って、図-61では、帰りの宇宙船はDから速度U(=-2V/(1+V2))でM迄を移動して、そのK系への投影点Nが地球への帰還点となります。
しかし、双子の兄弟の間には、悲しい事にこのように考察しても、線分MN分の虚時間(?)が横たわってしまうのです。
しかし、残念な事には今の私には、この虚数時間(?)の正確な実態がわかりません。
時間空間の時空面間の投影の際の係数は、ミンコフスキーの“各系における「固有時間」の値は一定である。”を使用しましたが、この結果として、図-61などで「虚数時間(?)」「時空回転角」を計算する際の係数をどのように扱うべきかが、明確でないのが残念であります。
但し、この『双子のパラドックス』を考える際、宇宙船の兄の時空を、「折り返し点まで行きの時空、折り返し点後帰りの時空」或いは、「折り返し点まで行きの時空、そして帰りもその時空」の2種類を考えましたが、当然この2種類の場合共々、地球で再開した際の双子の兄弟の間での虚数時間(?)の差は当然同じ筈です。
となりますと、同一時空内に居ても、虚数時間(?)が発生するという事なのでしょう。
従いまして、虚数時間(?)の座標軸は、敢えて図-63の如くに、時空面への垂直性に拘らずとも、図-62の如く虚数時空面を、実数時空面に垂直に考えても良いのではないでしょうか?
このように考えますと、光は、常に実虚数共々同じ値で進行してゆきます。
そして、K系における座標点(T,X)の虚時間空間は、図-61での計算に従って行うと、
虚数時間空間共々、(T+X)/2 を得る事になります。
更にこの結果驚くべき事に、同じ時空内の2点を比較した場合、その2点の時間が同じでも空間が異なれば、その空間の差分の1/2の虚空間が、空間が同じでも時間が異なれば、その時間の差の1/2の虚時間が存在してしまうのです。
又、双子の兄の宇宙船の帰路を、宇宙船の帰路の時空を往路とは別に考えた場合同様に、宇宙船の往路の時空での運動に置き換えて考えられた事は、宇宙船の帰路の時空を往路の時空に投影して考えた事に相当するのでしょう。
即ち、この宇宙船の帰路の問題は、同じ時空での移動(往路の時空での帰路への旅)とみなされることでも、実は、移動する事で元の時空から別の時空(往路の時空から帰路への時空)へ移行してしまう事を示しているのです。
(補足―2)赤道上と南北の極に置いた時計の相違は?
外国の物理学者が易しく物理科学を紹介しているNHKの教育テレビ番組の、「特殊相対性理論」中などで、“飛行機積み込まれて地球を何周かして来た原子時計は、特殊相対性理論で予測されるだけの時間の遅れが認められる。”と解説されていますが、飛行機は地球表面よりも数千メートルもの高度を飛行しますので、その際は、地球表面の原子時計と、飛行機中の原子時計では、地球から受ける重力に相違が生じます。
従って、この影響を考慮する必要があるのです。(特殊相対性理論よりも、一般相対性理論的に。)
更に、この実験の厳密性を確保するには、双子の宇宙飛行のように、地球を(仮の)中心として、反対方向に飛行する飛行機に原子時計を積み込むべきです。
東西に飛ぶと地球の自転の影響も加味されてしまうので、南北に飛んで比べることになるのでしょう。
それとも、原子時計を赤道上と、北極南極に置いて比べてみては如何なものでしょうか?
(或いは、双子の兄が赤道で暮らし弟が北極か南極で暮らしたとしたら、どちらがより年をとるのでしょうか?)
一般的に考えると、北極や南極に置かれた時計は、地球の自転には無関係に静止した状態とみなせますが、これらの時計に対して、赤道上に置かれた時計は地球の自転と共に、1日のうちに赤道を一周、即ち、時速:約1,700
kmという高速運動しているとみなせるでしょう。
その時速の計算は次の通りです。
先ずは、1日のうちに赤道を一周する速度ですから、その速度は、
2π(赤道半径)/(1日)
=2π×6378/(1日)=40053.84
km /(1日)=1668.91
km /(時間)
(∵ 赤道半径= 6378km)
しかし、赤道上に置かれた時計の立場になって考えると、その時計は静止しているのに、北極南極に置かれている時計が、逆に時速:約1,700
kmという高速運動していると観測するでしょう。
それでは、これらの時計のどの時計が進むのでしょうか?
又、双子の兄と弟ではどちらがより年をとってしまうと言うのでしょうか?
『なっとくする相対性理論』の著者の松田卓也さん、『時空図で理解する相対性理論』の著者の和田純夫さん、教えていただけますか?
(補足:3)「特殊相対論」と「一般相対論」
『なっとくする相対性理論』の著者の松田卓也さん、『時空図で理解する相対性理論』の著者の和田純夫さん共々、又、おかしな解説をなさって下さいます。
お二方とも、“『双子のパラドックス』は、「特殊相対論」でも「一般相対論」でも解決される”と 、先ずは松田氏の記述を下記に抜粋させて頂きます。
| ……双子のパラドックスの解決は、特殊相対論の範疇にある。しかし,一般相対論を用いて解決しようとする教科書や解説書もある(代表的な例はメラーの教科書)。それらの書物は,兄が反転するとき,現実問題としては一挙には反転できず,加速度運動をして徐々に反転するからである,としている。その反転している期間にはみかけの力が働く。この力は(せまい領域では)重力と区別できないというのが,一般相対論の基本の「等価原理」である。……重力場のあるところでは時計の進みは遅れるという効果がある。このため,ロケットに乗った兄の時計は反転時に遅れる,あるいは同じことを逆に言えば,反転時に地球にいる弟の時計が急速に進むと解釈できる。…… |
ここでの松田氏の記述を図解しますと、図:62 のようになると思います。
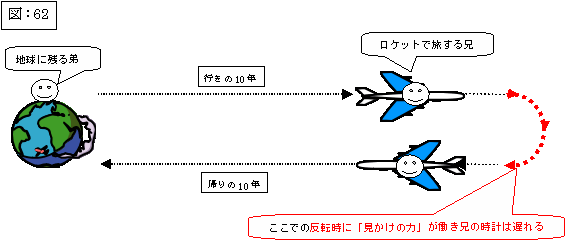 |
如何でしょうか?
私は、この一般相対論での「双子のパラドックス」の解釈は納得致します。
だとしますと、特殊相対論での“行きの10年、帰りの10年の間に生じる兄弟間の時計のズレ”は何処へ行ってしまうのですか?”
それとも、ここで記述しました一般相対論による“兄弟の時計のズレ”に、松田、和田氏による特殊相対論での“行きの10年、帰りの10年の間に生じる兄弟間の時計のズレ”を加算するというのですか?
更に、和田氏は“いい時計をもっている人は、飛行機に乗ったときは気をつけたほうがいい。1時間に約1億分の1秒ほどすすむ。”そして、ー般相対性理論で解釈すると、 “飛行機は地表から離れているので(重力は少なくなり)時間が早く進む”更に、特殊相対性理論で解釈するなら“飛行機の速度は、地表の自転の速度と違うから時間の進み方も違う”旨を記述されておられます。
斯くの如く両氏の“同一現象を特殊相対論でも一般相対論でも解釈可能”との表現は大変不思議です。
即ち、もしも表現の辻褄を合わせるのならば“「双子のパラドックス」(「飛行機の時計の遅れ」)は、特殊相対論と、一般相対論を併用する事で初めて解釈可能となる”と表現を改めなくてはなりません。
となりますとますます変になります。
何故なら、“「双子のパラドックス」は、特殊相対論と、一般相対論を併用する事で初めて解釈可能となる”と言うのであれば、「一般相対論は特殊相対論の領域に踏み込む事が出来ない」との珍説を提示しなくてはならなくなってしまいます。
特殊相対論の領域は、一般相対論では“「見かけの力」がゼロ(或いは、無限小)の場合”に相当する筈です。
従いまして、「双子のパラドックス」等が一般相対論で解釈出来るという事は、“「双子のパラドックス」等の現象を特殊相対論で解釈するのは不適”という事に落ち着くのだと思います。
更に、駄目を押す意味で、松田氏の先の抜粋文中の“ロケットに乗った兄の時計は反転時に遅れる,あるいは同じことを逆に言えば,反転時に地球にいる弟の時計が急速に進むと解釈できる”との現象が起こるのならば、地球からロケットが打ち上げられるたびに、地球上の時計は全て狂ってしまいます。
(松田氏の論に拠りますと、その上、重力も変化するという事なのでしょう。)
ロケットが打ち上げられずとも、どんなに遠方の天空の星々が、爆発などでその動きを急速に変化させると、(或いは、惑星の公転運動にはいわゆる遠心力が関係していますから)地球上の時計は(星々との距離に無関係に)それらの影響を受け、又、重力の変化を生じてしまう事になります。
誠におかしいと存じます。