新『コロンブスの電磁気学』(第8巻)
「アースに対する誤解」へのご案内
2019年2月4日 宇佐美 保
| 窓文社 〒151-0051 東京都渋谷区千駄ヶ谷5-2-4-402 電話 (03)3355-6265 FAX (03)3355-6270 |
本著は、別冊「新『コロンブスの電磁気学』(第3巻 縦列接続の登場)」中の『第11章 隣接伝送路へのマイナス反射波の発生に関する考察』に於ける考察が不十分で(と申しますか、不適切でも)ありましたので、この件に関して、更なる実験測定を繰り返し考察し直し、新たに“隣接伝送路へのマイナス反射波の発生に関する”理論構築を行いました。
この結果、隣接伝送路、そして、その伝送路を構成する信号線/グランド線が、入力伝送路の信号線/グランド線とペアを組む伝送路ともなり、共に、縦列接続の関係を有しつつ、入力伝送路に並列接続された伝送路であることをはっきりと確認できました。
そして、この関係が、各伝送路の信号線/グランド線間に誘電体が挿入された伝送路系(一般的には、ガラスエポキシ基板の両面に導体を配置した伝送路系)に於いても、生じる関係であることも確認しました。
従って、隣接伝送路(等)から、特定の周波数に限定されずに、一寸した細工で、入力信号と同形の電圧波形を有する出力信号が得られることも判明しました。
その上に、二本の導体の隣接伝送路ではなく、一本の導体のみでも、電磁界(電磁子、並び、電界子)の渦の中に置かれる状態で、その一本の導体にも、電流が流れることも確認できました。
このような状況からも、“電流とは、導体内の電子とか電荷の移動”ではなく、“電流は、導体の有する反磁性的性質(合わせて自由電子)と、導体に向かう電磁子集合体(一般的には電磁波と考えられている)との共同作業の結果発生する現象”であることがはっきりと確認されるのです。
更には、「アースを有する電源等に於ける、アースの問題点」は実験測定しつつ、その問題点も指摘しました。
従って、少なくとも電気の本質を探究するには、先ずは「アース」の問題を避ける(「アース」を無くす)ことが必要と存じます。
(但し、現状では「アース」を無くすことが、一般的に困難なので、本著では電圧の観測は差動プローブ(これでも、不十分な状態はありますが)を用いて行っております)
(両伝送路の信号線同士、又、グランド線同士の導体間隔も同様に、約0.7mmとしました)
|
| 写真:1 |
 |
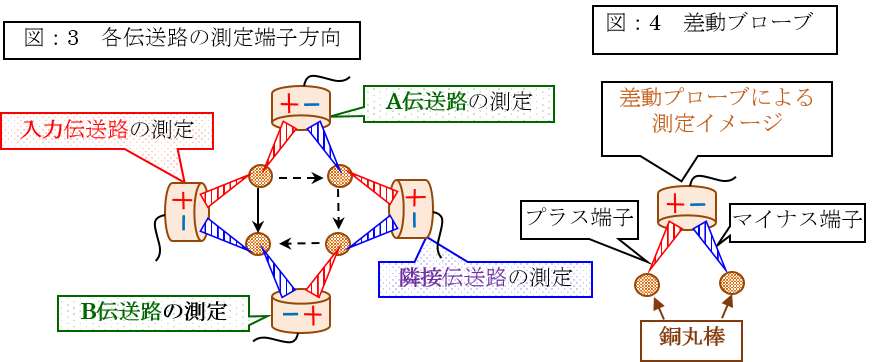
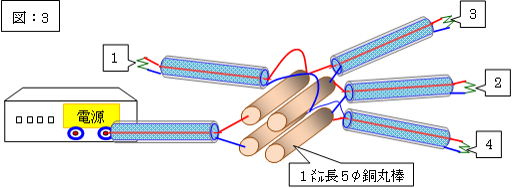
更に、電源(パルスジェネレータ)から入力伝送路へ電気信号を入力した場合の各伝送路に於ける電圧測定の際には、差動プローブの先端を次の「図:3」のように接触しました。
(この伝送路系の概略図は、先の「図:1」を正面から見た状態に相当致します。
そして、先の図中の記述のように、「A伝送路」は「入力/隣接伝送路の信号線同士」、「B伝送路」は「入力/隣接伝送路のグランド線同士」が形成する伝送路です)
 |
このように各伝送路の電圧変化を同時に測定することで“入力伝送路並び隣接伝送路の各信号線が形成する「A伝送路」と、「隣接伝送路」、並びに、入力伝送路並び隣接伝送路の各グランド線が形成する「B伝送路」の3組の伝送路が縦列接続された状態で、「入力伝送路」に対して、並列接続されている”事実が「本章」に於いて実証されるのです。
(注:パルスジェネレータから入力電流共々出力されるトリガー電流のオシロスコープへの到達時点を基準として、1本の差動プローブによる各測定結果の同時性を確保しました)
| 表:2 電圧変化測定結果の上からの表示順序(500mV/目盛 2ナノ秒/目盛) |
|
1)入力伝送路 2)(4)+(5)+(6)(縦列接続された伝送路の電圧変化の和) 3)(1)-(2)(「入力伝送路の電圧変化」-「縦列接続された伝送路の電圧変化の和」) 4)A伝送路(信号線同士) 5)隣接伝送路 |
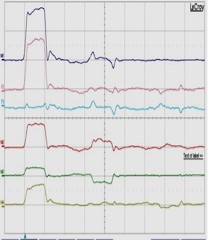
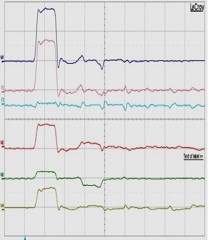
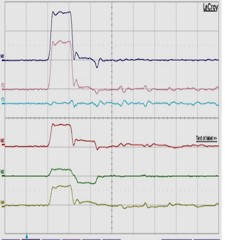
| 測定結果:4 入力伝送路末端&隣接伝送路近端に50Ω抵抗体をセット | ||||
| 測定結果:4-1 隣接伝送路末端(遠端):50Ω抵抗体で整合終端処理 | ||||
| 0cm地点 | 33.3cm地点 | 66.7cm地点 | 100cm地点 | |
| 1)入力伝送路 2)(4)+(5)+(6) 3)(1)-(2) 4)A伝送路(信号線同士 6)B伝送路(グランド線同士) |
 |
 |
 |
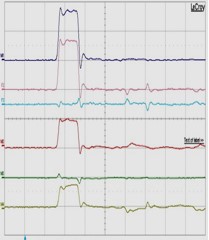 |
この結果に見ますように、前著で確認されたと同様に
“「(1)入力伝送路」の電圧波形(電圧値)と縦列接続の関係を有するこれら3組の「A、隣接、B」伝送路との伝送路の電圧波形の合算値、
即ち「(2)「(4)+(5)+(6)」に等しい事(両者が並列関係にある)が、伝送路上の観測位置を変化させても、同様に確認することが可能です。
この背景として、1)~6)の測定結果の内、特に、表示された結果の上から3段目の(3)表示値が常にゼロであることに注目して下さい。
(∵ (3)=(1)-(2)=0)
(即ち、(1):「入力伝送路」の電圧波形(電圧値)
=
(2):各「A、隣接、B」伝送路の電圧波形(電圧値)の合算値)
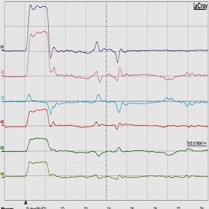
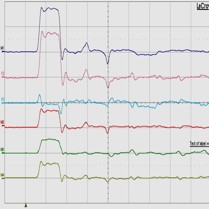
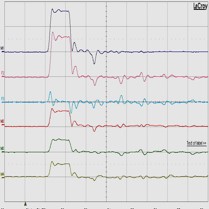
| 測定結果:5 隣接伝送路近端、並び、遠端をオープン状態にした場合 | ||||
| 測定結果:5-1 入力伝送路末端:50Ω抵抗体で整合終端処理 | ||||
| 0cm地点 | 33.3cm地点 | 66.7cm地点 | 100cm地点 | |
| 1)入力伝送路 2)(4)+(5)+(6) 3)(1)-(2) 4)A伝送路(信号線同士) 6)B伝送路(グランド線同士) |
 |
 |
 |
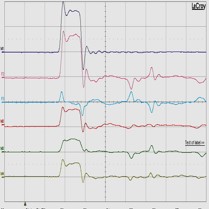 |
|
測定結果:5 (各 500㍃秒/目盛) |
|
|
1)入力伝送路(1番目) (1V/目盛) 2)合算値(=4)+5)+6)) (1V/目盛) 4)信号線同士伝送路(3番目) (500mV/目盛) 5)隣接伝送路の末端(2番目) (500mV/目盛) |
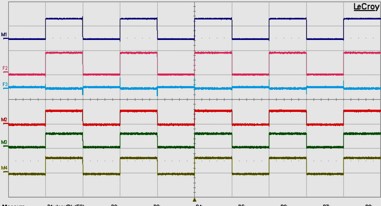 |
何故こうなるか等は本著をご覧ください。
“別冊「新『コロンブスの電磁気学』(第3巻 縦列接続の登場)」に於ける『隣接伝送路へのマイナス反射波の発生に関する考察』が不十分でしたので、本著に於いて更なる実験測定の繰り返しを行い、考察し直すことによって、縦列接続理論構築”が完遂出来たと存じます。
この様な実験考察結果から、「ファラデーの電磁誘導説」とは全く無関係に、入力伝送路に発生する電磁波群の影響下に、隣接伝送路や、他の導体を置けば、入力伝送路の信号線、グランド線とに対して、それら新たに置かれた導体が伝送路を組みつつ、その伝送路に電流が流れるのです。
そして、その電流らは縦列接続の関係を保ちつつ、入力伝送路の電流に対して、並列接続の関係を有つつ流れるとこが明確化されるのです。
ところが、これらの電圧の状態を、従来の一般的な電圧測定器であるオシロスコープでは、はっきりと明示されないのです。
(この詳細は、本文『第7章 第2節 オシロスコープに全ての端子を接続した場合』をご参照下さい)
そして、前著(第3巻)『ファラデー 電気実験(上) M.Faraday著 監修者:田中豊助 (株)内田老鶴圃』にも記述した、今ほどの測定技術を有さなかったファラデーご自身の言葉は“すべての電流には必ずその流れに対して直角に,相応した強さの磁気作用を伴うものであるにもかかわらず,電気の良導体をこの作用圏内においても,その中に何らの電流も誘起されないし,またこのような電流に相当する効果が少しも感知されないということは,はなはだ異様なことに思われた。”と書かれています。
従って、「ファラデーの電磁誘導式」が、一般常識となり、現在のオシロスコープを従来的な方式で使用しても、それを覆すことが出来ずに、そして又、“アースは常にゼロボルト”の迷信が確立も、今以って信じ続けられているのです。
どうか本著を熟読され(また、熟読されたお方は)、「ファラデーの電磁誘導式」や「アースはゼロボルト」の迷信などから、きっぱりとお分かれの程をお願い致します。