�V�w�R�����u�X�̓d���C�w�x�i��5���j
�u�V���ȃg�����X���_�v�ւ̂��ē�
2015�N8��23���@�F�����@��
| ������ ��151-0051�@�����s�a�J���ʃ��J5-2-4-402 �d�b�@�i03�j3355-6265 FAX�@�i03�j3355-6270 |
�܂�����
�@�w�t�@���f�[ �d�C�����i��j M.Faraday�� �ďC�ҁF�c���L���i���j���c�V�ߕށx�ɂ́A���̋L�q�����܂��B
�c�c�d�C�̗Ǔ��̂����̍�p�����ɂ����Ă��C���̒��ɉ���̓d�����U�N����Ȃ����C�܂����̂悤�ȓd���ɑ���������ʂ����������m����Ȃ��Ƃ������Ƃ́C�͂Ȃ͂��ٗl�Ȃ��ƂɎv��ꂽ�B
�@���̂悤�Ȍ��ʂ��l���邱�ƁC���Ȃ킿�ʏ�̎��C����d�C�悤�Ɗ��҂��邱�Ƃ��C�d���̊������ʂ̎����I�����ɑ��Ď�X�̏ꍇ�Ɏ����܂����̂ł������B�����čŋ߂ɂȂ��Ď��͍m��I�Ȍ��ʂɂ��ǂ�����Ƃ��ł����B�c�c
�@�������A�w��3�́x�ȍ~�̎����l�@����A�g�t�@���f�[���ٗl�Ȃ��Ǝv�����h���́A�t�@���f�[����̓d�C����@�킪�s�\���ł��������Ƃ��匴���ł����āA���ۂɂ́A�g�d�C�̗Ǔ��̂����̍�p�����ɂ��������h���̗Ǔ��̂ɓd�����U�N�����̂ł��B
�]���āA���̈��p���̌㔼�́g�ʏ�̎��C����d�C�悤�h�Ƃ̎��݂́A�u�}�N�X�E�F���̓d���g�̗\�z�v�ȑO�̃t�@���f�[�ɂ́A�u�d���g�v�̑��݂�m��R���Ȃ��A�u���C�̂݁v�ɒ��ڂ����̂ł��傤�B
����ł��A�t�@���f�[�̓����̎v���Ƃ͕ʂ̎��p�I�ȁu�g�����X�v�̌��^�ݏo���u�̑�ȋƐсv�ɔ��W�����̂ł��B
�i���́g�t�@���f�[�̓����̎v���Ƃ͕ʁc�c�h�Ɋւ��錏�́A��́w��9�� �t�@���f�[���g�̃g�����X�Ɋւ�������x�����Q�Ƃ��������j
�@�ܘ_�A�����܂Ŏ����l�@���Ă��܂����ʂ�ɁA�u�t�@���f�[�̓d���U���̖@���v�͌���̎Y���ł�����A�g�����X�̌������u�t�@���f�[�̓d���U���̖@���v�Ƃ͓��R���W�ł��B
�����A�g�����X�Ɋւ��āA�w�����ォ������Ă����^��́g�g�����X�̃R�C���������A�V���[�g��Ԃ̓d���Ȃ̂ɁA���̃g�����X��������o���Ȃ��̂��H�h�ł����B
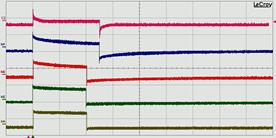
�@�����A�g�����X�ɁA���g����0.1Hz�i������10�b�ŁA���M���Ԃ�5�b���j�̋�`�g�i����������j����͂���ƁA��́w��2�́x�́u���茋�ʁF1�v�̃R�C���o������̓d���́A�[���{���g�ƂȂ��Ă��܂�����A�V���[�g��Ԃł��B
�������A����̎����ł̓��͓d����1�{���g�ł�������A�͐����܂���ł������A100�{���g���������ς������ł��傤�B
�����ŁA�����g�p���Ă���g�����X����́A�����o���Ă��邱�Ƃ͂Ȃ��A�g�����X�Ƃ��ċ@�\���Ă���邩�̋^����A�{���ɂĉ𖾂��čs���܂��B
�{���������������O�ɁA���̋L�q���ю����A�v�Z���ʂɂ��ڒʂ����������B
�g�����X����͒����i��`�g�M���j����{
�قȂ���g���̋�`�g��1�p���X�i1V/0V�j�݂̂��g�����X��1�����R�C���֓��͂����ۂ́u���茋�ʁv�Ƃ��āA���́g���`�̓d���g�`�������ɓ�����h�̂ł��B�ォ��A0.1Hz�A10Hz�A50Hz�A250Hz�A500Hz�̑��茋�ʂł��B
|
1�����������d���ω��@�i�e�@2V/�ڐ��j |
2�����o�͓d���ω��@�i�e�@1V/�ڐ��j |
|
|
|
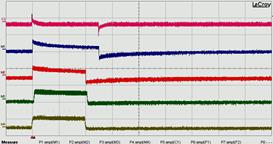
�X�ɁA1�p���X��10Hz�i��`�g�j�̐M���̑S�́iOFF�ƂȂ閘�j���\�������悤�ɁA���Ԏ��̒P�ʂ�1�ڐ�10�~���b�ɓ��ꂵ�āA���́u���茋�ʁv�������܂��B
|
|
|
�@���̑��茋�ʂ���A�g�����X�̋�`�g�M���ɑ��铮��́A�������͂ɂ�铮�쒆�̂��鎞�ԂɁA���̒������͂��~���Ă��܂������ۂƓ����ł��邱�Ƃ�������܂��B
�����āA���̌��ۂ���A�������~������������i�����ɒZ�����Ԃ̌���͂��ĊJ����A�������͂��p���������ƂƂȂ�A���̓���͉��x����Ă��������ʂނł��傤�B
�]���āA���̂悤�ɁA�u�O���t�F1�v�̒Z�����̋�`�g�̌��ʂ���A�u�O���t�F2�v�̒������̋�`�g�M���i�X�ɂ́A�u�O���t�F3�v�̃T�C���g�M���j���i�v�Z�\�t�g�wExcel�x��p���āj�������邱�Ƃ��\�ł��B
|
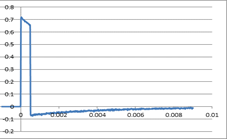
�O���t�F1�@1KHz�̋�`�g�M���̏o�� |
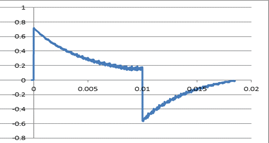
�O���t�F2�@40���Z����50Hz�̏o�͔g |
|
|
|
�u�O���t�F3�v�́A36���Z����ہA��{�d���l�i�O���t�F1�j�ɑ�1�p���X�ڂ�sin10���A��2�p���X�ڂ�sin20���A��3�p���X�ڂ�sin30���c�c��36�p���X�ڂ�sin360���Ə����T�C���l���悶�Čv�Z���s���܂����B
| �O���t�F3�@36���Z���� 55.6Hz�̃T�C���g |
�Q�l�p�̎����l 55.6Hz�̃T�C���g�o�� |
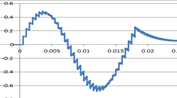 |
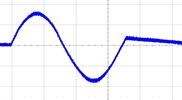 |
�i�Q�l�ׂ̈ɁA�u�Q�l�p�̎����l�v�����킹�Čf���܂������A���Z�l�Ƃ̗ǂ����v�����F�߂��܂��j
�ł́A�{�����玟�̏͂��f���܂��傤�B
��10�́@�c��ڑ����ꂽ���̊ۖ_�`���H�ł̑��茋��
�{���ʼn𖾂��Ă����g�g�����X�̍��{�����́A�c��ڑ��c�c�h�̘_���A�X�Ɋm������̂Ƃ���ׁA�ʍ��w��3�� �c��ڑ��̓o��x�ɉ�����w��11�� �⑫�F3 ���͕��їאړ`���H�̖��[��Ԃ�ω��������ꍇ�x�̎������ʓ����ȉ��ɍČf�������܂��B
�i���́A���̂悤�Ȏ������ʂɂȂ邩�̍l�@���̏ڍׂ́A�ʍ��w��3���x����Q�Ɖ������j
���̊ۖ_�i���a�F5mm�A�����F1�b�j��4�{�p���č\�������u�}�F1�v�̂悤�ȓ��͓`���H�ƁA����ɏc��ڑ�����אړ`���H�ɉ����āA�����`���H�iZ=��50���j�̖��[���A���͓`���H���[�����A50����R�Ő����I�[���������ꍇ�A�V���[�g��Ԃ̏ꍇ�A�I�[�v����Ԃ̏ꍇ�ƕω������A����ɉ����Ċe�ꍇ�Ƃ��A�אړ`���H�̖��[�������A�e�X�A�V���[�g��ԁA50���I�[������ԁA�I�[�v����Ԃƕω������āA�e�X�̏ꍇ�Ɋւ��āA�d���i�p���X�W�F�l���[�^�j����A���͓`���H�ցA250MHz�i1V/0V�j��1�p���X�̋�`�g�A���тɁA75MHz�i�ꍇ�ɂ���ẮA37.5MHz�j�̋�`�g�̘A���g����͂��A�אړ`���H�ߒ[���̓d���ω��������v���[�u�ő��肵�A���̌��ʂ܂����B
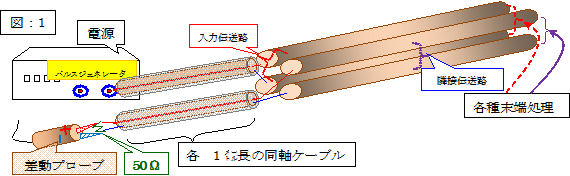 |
�@
�悸�́A���͓`���H���[��50����R�Ő����I�[���������ꍇ�́u�}�F1�v�̑��茋�ʂł��B
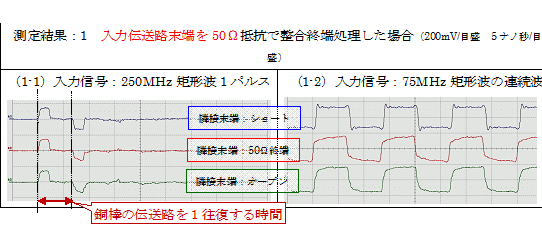 |
���͓��͓`���H���[���V���[�g��ԂƂ����ꍇ�̗אړ`���H�ł̑��茋�ʂł��B
 |
�@�Ō�����͓`���H���[���I�[�v������Ƃ����ꍇ�̗אړ`���H�ł̑��茋�ʂł��B
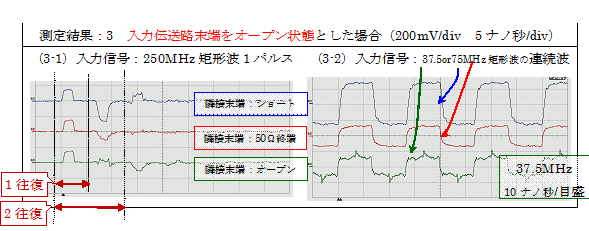 |
�ȏ�̑��茋�ʂ���A���͓`���H���ɓ��͂��ꂽ�d���ɂ���āA�c��ڑ��W�ɂ���אړ`���H�̋ߒ[���[�o���ւƓ��͓d���Ɠ��`�̓d�����U������錻�ۂ̑��݂ƁA�X�ɂ́A���[���������d�������͕��їאړ`���H�̉��[�̏ɉ����āA�}�C�i�X���̓v���X�d���Ƃ��ċt�����ė�����A���͓`���H���[���I�[��������Ă��Ȃ��ꍇ�ɂ́A���̓��͓`���H�ɔ�������t���d���ɂ���āA���͓`���H�̓��͕��ŁA�אړ`���H�ւƐV���ȓd�������邱�ƂƂȂ�܂��B
�@�����āA�����̌��ۂ͂����܂Ŏ������l�@���Ă����A�c��ڑ��ɋN�����錻�ۂł���A�{�͂ōl�@���ė��܂����u�אړ`���H�ւ̃}�C�i�X���˔g�̔����Ɋւ���l�@�v�ɑ������錻�ۂł���̂ł��B
�ܘ_�A���͓`���H�̖��[�ɂ���ẮA�i�c��ڑ��̉������@�ɂ���Ắj�A�u�אړ`���H�փ}�C�i�X���˔g�ł͂Ȃ��A�v���X�g�̔�����������v�Ƃ������ƂȂ�܂��B
�@���̂悤�ȒP���ȁA�������A�R�C�����l�ɓ���/�אړ`���H�̖��[���V���[�g��Ԃ̏ꍇ���܂߂��`���H�\���̎���������g�g�����X�̍��{�����́A�c��ڑ��h���������܂��B
�ڎ�
�܂����� 1
��1�́@�g�����X����Ɓu�t�@���f�[�̓d���U���̖@���v�Ƃ̖��� 2
��2�́@�g�����X�͋�`�g�M���ł����삷�� 5
��3�́@��`�g�M���Ńg�����X�̓�����m�F 6
��4�́@�g�����X�̓���͒����M���i��`�g�M���j����{ 8
��5�́@�g�����X�̓���͒����M���i��`�g�M���j����{���v�Z�\�t�g�Ŋm�F 10
��6�́@�P�ƃR�C���ƃg�����X�Ƃ̗ގ��� 12
��7�́@�g�����X�ƒP�ƃR�C���̗ގ����̍Ċm�F 14
��W�́@�ʃg�����X��p���Ă̑��茋�� 17
��9�́@�g�����X�ƘA���g�̊W 19
��10�́@�c��ڑ����ꂽ���̊ۖ_�`���H�ł̑��茋�� 22
��11�́@��ʓd������`���H�Ƃ��Ă̌��� 24
��12�́@��ʓd�����R�C����� 27
��12�́@��1�߁@�R�C���̕��������� 27
��12�́@��2�߁@�R�A�ނ̌��� 29
��13�́@�t�@���f�[���g�̃g�����X�Ɋւ������ 30
��14�́@�g�����X�ɉ�����R�A�ނ̖��� 35
��14�� ��1�߁@�t�F���C�g���g�����X�̃R�A�ɗp�����ꍇ 39
�⑫�F�����v���[�u�̃v���X�[�q�݂̂̑��� 41
��14�́@��2�߁@�`���H�ɑ���t�F���C�g�̉e�� 42
��14�́@��3�߁@�p�[�}���C��p���Ă̗\���I�Ȏ��� 44
��15�́@�g�����X�̓��o�͓d���ƃR�C���̊�������̊W 47
��16�́@�g�����X�ɑ����ʓI�F���̈�� 49
��17�́@�g�����X�̓d�͑��� 50
��17�� ��P�߁@�g�����X�����ł̑��� 50
��17�� ��2�߁@���d���̑��� 50
��18�́@�����p�g�����X 54
���Ƃ��� 55